2026年同步练习江苏九年级数学下册苏科版第65页解析答案

12. 阅读下面的材料，先完成阅读填空，再按要求答题：
$ \sin 30^{\circ} = \frac{1}{2} $， $ \cos 30^{\circ} = \frac{\sqrt{3}}{2} $，则 $ \sin^{2} 30^{\circ} + \cos^{2} 30^{\circ} = $_______； $ \sin 45^{\circ} = \frac{\sqrt{2}}{2} $， $ \cos 45^{\circ} = \frac{\sqrt{2}}{2} $，则 $ \sin^{2} 45^{\circ} + \cos^{2} 45^{\circ} = $_______； $ \sin 60^{\circ} = \frac{\sqrt{3}}{2} $， $ \cos 60^{\circ} = \frac{1}{2} $，则 $ \sin^{2} 60^{\circ} + \cos^{2} 60^{\circ} = $_______.
……
观察上述等式，猜想：对任意锐角 $ A $，都有 $ \sin^{2} A + \cos^{2} A = $_______.
(1) 如图，在锐角三角形 $ ABC $ 中，利用三角函数的定义及勾股定理证明你的猜想；
(2) 已知 $ \angle A $ 为锐角( $ \cos A ＞ 0 $ )，且 $ \sin A = \frac{3}{5} $，求 $ \cos A $ 的值.

答案：
1 1 1 1
解：(1)过点B作BD⊥AC，垂足为点D

在Rt△ABD中，由勾股定理可得，$AB^2=AD^2+BD^2$
∵$sinA=\frac {BD}{AB}，$$cosA=\frac {AD}{AB}$
∴$sin^2A+cos^2A=\frac {BD^2+AD^2}{AB^2}=1$
(2)
∵$sinA=\frac 35，$$sin^2A+cos^2A=1$
∴$cos^2A=1-sin^2A=\frac {16}{25}$
∵∠A为锐角(cosA＞0)
∴$cosA=\sqrt {\frac {16}{25}}=\frac 45$

13. 如图，在 $ \triangle ABC $ 中， $ \angle C = 90^{\circ} $， $ D $ 是 $ BC $ 上的一点， $ \angle ADC = 45^{\circ} $， $ BD = 2DC $. 求 $ \cos B $ 和 $ \sin \angle BAD $ 的值.

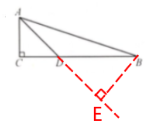
答案：
解：过点B作BE⊥AD，交AD的延长线于点E

设DC=x，则BD=2x，BC=BD+DC=3x
∵∠ADC=45°，∠C=90°
∴△ACD是等腰直角三角形
∴AC=DC=x
在Rt△BCD中，∵BC=3x，AC=x
∴$AB=\sqrt {BC^2+AC^2}=\sqrt {10}x$
∴$cosB=\frac {BC}{AB}=\frac {3x}{\sqrt {10}x}=\frac {3\sqrt {10}}{10}$
∵∠BDE=∠ADC=45°，BE⊥AD
∴△BDE是等腰直角三角形
∵BD=2x
∴$BE=DE=\frac {BD}{\sqrt 2}=\sqrt 2x$
∵△ACD是等腰直角三角形，CD=x
∴$AD=\sqrt 2CD=\sqrt 2x$
∴$AE=AD+DE=2\sqrt 2x$
在Rt△ABE中，∵$AE=2\sqrt 2x，$$BE=\sqrt 2x$
∴$AB=\sqrt {AE^2+BE^2}=\sqrt {10}x$
∴$sin∠BAD=\frac {BE}{AB}=\frac {\sqrt 2x}{\sqrt {10}x}=\frac {\sqrt 5}5$
综上所述，$cosB=\frac {3\sqrt {10}}{10}，$$sin∠BAD=\frac {\sqrt 5}5$