11. 在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ a $、$ b $、$ c $ 分别表示 $ \angle A $、$ \angle B $、$ \angle C $ 的对边,$ \tan A = \frac{3}{4} $,$ c = 5\sqrt{13} $. 求 $ a $、$ b $.
答案:解:设a=3x
在Rt△ABC中,∵$tan A=\frac {a}b=\frac 34,$a=3x
∴b=4x
∴$c=\sqrt {a^2+b^2}=5x$
∵$c=5\sqrt {13}$
∴$5x=5\sqrt {13}$
解得$x=\sqrt {13}$
∴$a=3x=3\sqrt {13},$$b=4x=4\sqrt {13}$
12. 如图,在 $ \triangle ABC $ 中,$ \angle A = \alpha $,$ \angle B = \beta $,$ CD ⊥ AB $,垂足为 $ D $,且 $ CD = h $. 求 $ AB $ 的长.

答案:解:在Rt△ACD中,∵∠A=α,CD=h
∴$tan α=\frac {CD}{AD}$
∴$AD=\frac {CD}{tan α}=\frac {h}{tan α}$
同理可得$BD=\frac {CD}{tan β}=\frac {h}{tan β}$
∴$AB=AD+BD=\frac {h}{tan α}+\frac h{tan β}$
13. 在 $ \triangle ABC $ 中,$ AB = AC $,$ CH $ 是边 $ AB $ 上的高,且 $ CH = \frac{3}{5}AB $. 求 $ \tan B $ 的值.
答案:解:分两种情况
①当△ABC为锐角三角形时
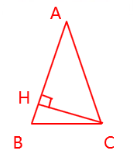
在Rt△ACH中,∵AC=AB,$CH=\frac 35AB$
∴$AH=\sqrt {AC^2-CH^2}=\frac 45AB$
∴$BH=AB-AH=\frac 15AB$
在Rt△BCH中,∵$CH=\frac 35AB,$$BH=\frac 15AB$
∴$tan B=\frac {CH}{BH}=3$
②当△ABC为钝角三角形时
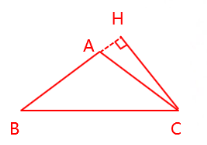
同理,$AH=\frac 45AB$
∴$BH=AB+AH=\frac 95AB$
在Rt△BCH中,∵$CH=\frac 35AB,$$BH=\frac 95AB$
∴$tan B=\frac {CH}{BH}=\frac 13$
综上所述,tan B的值为3或$\frac 13$