5. (1) 根据图中的条件,分别求出 $ \angle A $、$ \angle B $ 的正切值.
(2) 观察第(1)题的计算结果,你发现了什么?请写出你发现的结论.

]
答案:解:$(1)①tan A=\frac {BC}{AC}=\frac 34,$$tan B=\frac {AC}{BC}=\frac 43$
②在Rt△ABC中,∵AB=13,AC=5
∴$BC=\sqrt {AB^2-AC^2}=12$
∴$tan A=\frac {BC}{AC}=\frac {12}{5},$$tan B=\frac {AC}{BC}=\frac {5}{12}$
③在Rt△ABC中,∵AB=25,AC=24
∴$BC=\sqrt {AB^2-AC^2}=7$
∴$tan A=\frac {BC}{AC}=\frac {7}{24},$$tan B=\frac {AC}{BC}=\frac {24}{7}$
(2)当∠A+∠B=90°是,tan A · tan B=1,即互余两角的正切互为倒数
6. 在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ AB = 5 $,$ AC = 3 $,则 $ \tan A = $
$\frac{4}{3}$
,$ \tan B = $
$\frac{3}{4}$
.
答案:$\frac {4}{3}$
$\frac {3}{4}$
7. 如图,在 $ \mathrm{Rt} \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ CD $ 是斜边 $ AB $ 上的高. $ \tan A $ 有三种表达方式:$ \tan A = \frac{CD}{AD} = \frac{(\ \ \ \ )}{(\ \ \ \ )} = \frac{(\ \ \ \ )}{(\ \ \ \ )} $.

答案:BC
BD
AC
CD
8. 如图,在 $ \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ CD $ 是高,$ BC = 3 $,$ AC = 4 $,则 $ \tan \angle BCD $ 的值为
$\frac{3}{4}$
.

答案:$\frac {3}{4}$
9. 如图,在正方形网格中,点 $ O $、$ B $ 都在格点上,$ OA $ 经过格点 $ P $,则 $ \tan \angle AOB $ 的值为(
D
).

A.$ \frac{\sqrt{5}}{5} $
B.$ \frac{2\sqrt{5}}{5} $
C.$ \frac{1}{2} $
D.$ 2 $
答案:D
10. 在 $ \triangle ABC $ 中,$ AB = AC = 10 $,$ BC = 12 $. 求 $ \tan C $ 的值.
答案:解:过点A作AD⊥BC,垂足为点D
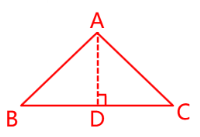
∵AB=AC=10,AD⊥BC
∴△ABC是等腰三角形,点D是BC的中点
∵BC=12
∴$CD=\frac 12BC=6$
在Rt△ACD中,∵CD=6,AC=10
∴$AD=\sqrt {AC^2-CD^2}=8$
∴$tan C=\frac {AD}{CD}=\frac 43$