9. 如图,在 $\triangle ABC$ 中,$DE// BC$,$\frac{AE}{EC}=\frac{1}{2}$. 求 $\triangle DOE$ 与 $\triangle BOC$ 的周长比与面积比.

答案:解:∵DE//BC
∴△ADE∽△ABC
∴$\frac {DE}{BC}=\frac {AE}{AC}$
∵$\frac {AE}{EC}=\frac 12$
∴$\frac {DE}{BC}=\frac {AE}{AC}=\frac 13$
∵DE//BC
∴∠ODE=∠OCB
∵∠DOE=∠BOC
∴△DOE∽△BOC,且相似比为1 : 3
∴△DOE与△BOC的周长比为1 :3,面积比为1 :9
10. 如图,在梯形 $ABCD$ 中,$AD// BC$,$\triangle AOD$ 的面积与 $\triangle BOC$ 的面积之比为 $1:9$,$\triangle AOB$ 的面积为 $6$.
(1) 求 $AD:BC$ 的值;
(2) 求梯形 $ABCD$ 的面积.

答案:解:(1)∵AD//BC
∴∠DAO=∠OCB
∵∠AOD=∠BOC
∴△AOD∽△COB
∵△AOD的面积与△BOC的面积之比为1:9
∴AD:BC=1:3
(2)∵△AOD∽△COB,AD:BC=1:3
∴OD:OB=AD:BC=1:3
∴$S_{△AOD}$:$S_{△AOB}=1$:3
∵△AOB的面积为6
∴$S_{△AOD}=2,$$S_{△ABD}=8$
∵$S_{△ABD}$:$S_{△BCD}=AD$:BC=1:3
∴$S_{△BCD}=24$
∴$S_{梯形ABCD}=S_{△ABD}+S△ BCD=32$
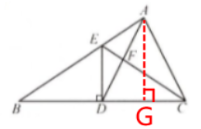
11. 如图,在 $\triangle ABC$ 中,$D$ 是边 $BC$ 的中点,且 $AD = AC$,$DE⊥ BC$ 交 $AB$ 于点 $E$,$EC$ 交 $AD$ 于点 $F$. 若 $\triangle FCD$ 的面积为 $5$,$BC = 10$,求 $DE$ 的长.

答案:解:作AG⊥BC,垂足为G
∵AD=AC
∴∠ACB=∠FDC
∵点D是BC的中点
∴DB=DC
∵DE⊥BC
∴∠EDB=∠EDC=90°
在△BDE和△CDE中
$\begin{cases}{DE=DE}\\{∠EDB=∠EDC}\\{DB=DC}\end{cases}$
∴$△BDE≌△CDE(\mathrm {SAS})$
∴∠FCD=∠ABC
∵∠FDC=∠ACB
∴△FCD∽△ABC,且相似比为CD:BC=1:2
∴$S_{△ABC}=4S_{△FCD}$
∵$S_{△FCD}=5$
∴$S_{△ABC}=\frac 12×BC×AG=20$
∵BC=10
∴AG=4
∵点D为BC的中点
∴BD=CD=5
∵AD=AC,AG⊥BC
∴点G为CD的中点,$DG=\frac 12CD=\frac 52$
∴$BG=BD+DG=\frac {15}{2}$
∵DE⊥BC
∴DE//AG
∴△BDE∽△BGA
∴$\frac {BD}{BG}=\frac {DE}{AG}$
∵BD=5,$BG=\frac {15}{2},$AG=4
∴$\frac 5{\frac {15}{2}}=\frac {DE}4$
∴$DE=\frac 83$
12. 如图,在 $\triangle ABC$ 中,点 $D$、$E$ 分别在 $AB$、$AC$ 上,且 $DE// BC$(点 $D$ 不与点 $A$、$B$ 重合). 设 $\frac{AD}{AB}=x$,$\triangle DBE$ 的面积为 $y$,$\triangle ABC$ 的面积为 $5$,求 $y$ 关于 $x$ 的函数表达式,并写出自变量 $x$ 的取值范围.

答案:解:由△ADE∽△ABC,得$\frac {S_{△ADE}}5=(\frac {AD}{AB})^2=x^2,$
$S_{△ADE}=5x^2$
又$\frac y{S_{△ADE}}=\frac {BD}{AD}=\frac {AB-AD}{AD}=\frac {AB}{AD}-1=\frac 1{x}-1$
∴$y=(\frac 1{x}-1) · S_{△ADE}=(\frac 1{x}-1) · 5x^2=5x-5x^2$
∴$y=5x-5x^2(0<x<1)$