7. 如图,在$□ ABCD$中,$BE = 3$,$EF = 2$.
(1)求$DF:AB$的值;
(2)求$FG$的值.

答案:解:(1)∵四边形ABCD是平行四边形
∴AB//CD
∴∠BAE=∠ECF
∵∠BEA=∠CEF
∴△ABE∽△CFE
∴AB:CF=BF:EF=3:2
∴DF:AB=1:3
解:(2)∵四边形ABCD是平行四边形
∴AD//BC
∴∠G=∠FBC
∵∠DFG=∠BFC
∴△DFG∽△CFB
∴$\frac {FG}{BF}=\frac {DF}{CF}$
∵DF:AB=1:3
∴$\frac {FG}{BF}=\frac {DF}{CF}=\frac 12$
∵BF=BE+EF=5
∴$FG=\frac 52$
8. 如图,$\triangle ABC$是等边三角形,点$D$、$E$分别在边$BC$、$AC$上,且$BD = CE$,$AD$与$BE$相交于点$F$.
(1)写出一个与$\triangle AEF$相似的三角形,并证明.
(2)写出一个有关比例中项的结论:$AE^{2} =$_________$·$
BE·FE(也可AD·FE)
(不要求写出证明过程).

答案:BE
FE
解:(1)△AEF∽△ADC,证明如下:
∵△ABC是等边三角形
∴AB=BC=CA,∠BAE=∠C=60°
∵BD=CE
∴CD=AE
在△ACD和△BAE中
$\begin{cases}{CD=AE}\\{∠C=∠BAE}\\{AC=AB}\end{cases}$
∴$△ACD≌△BAE(\mathrm {SAS})$
∴∠ADC=∠BEA
∵∠EAF=∠DAC
∴△AEF∽△ADC
9. 如图,在正方形$ABCD$中,$AB = 2$,$P$是边$BC$上的一个动点(不与点$B$、$C$重合),$DQ⊥ AP$,垂足为$Q$.
(1)求证:$\triangle DQA\backsim\triangle ABP$.
(2)当点$P$的位置变化时,线段$DQ$的长也随之变化. 设$PA = x$,$DQ = y$,求$y$与$x$之间的函数表达式.

答案:(1)证明:
因为四边形$ABCD$是正方形,所以$\angle B = 90^{\circ}$,$AD// BC$。
所以$\angle D A Q=\angle APB$(两直线平行,内错角相等)。
又因为$DQ⊥ AP$,所以$\angle DQA = 90^{\circ}$。
则$\angle DQA=\angle B$。
在$\triangle DQA$和$\triangle ABP$中,$\{\begin{array}{l}\angle DQA=\angle B\\\angle DAQ=\angle APB\end{array} $。
根据两角分别相等的两个三角形相似,可得$\triangle DQA\backsim\triangle ABP$。
(2)解:
因为四边形$ABCD$是正方形,$AB = 2$,所以$AD = AB = 2$。
由(1)知$\triangle DQA\backsim\triangle ABP$。
根据相似三角形的性质:相似三角形对应边成比例,可得$\frac{DQ}{AB}=\frac{AD}{PA}$。
已知$PA = x$,$DQ = y$,$AB = AD = 2$,代入比例式$\frac{y}{2}=\frac{2}{x}$。
整理可得$y=\frac{4}{x}(2\lt x\lt2\sqrt{2})$。
综上,(1)已证$\triangle DQA\backsim\triangle ABP$;(2)$y$与$x$之间的函数表达式为$y = \frac{4}{x}(2\lt x\lt2\sqrt{2})$。
10. 如图,在$\triangle ABC$中,$D$是$BC$的中点,点$G$是$\triangle ABC$的重心. 求$\frac{AG}{AD}$的值.

答案:解:连接BG并延长与AC交于点E,连接DE
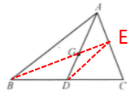
∵G 是△ABC的重心
∴BE是△ABC的中线,点E是AC的中点
∵点D是BC的中点
∴DE是△ABC的中位线
∴DE//AB,$DE=\frac 12AB$
∴∠ABG=∠GED
∵∠AGB=∠DGE
∴△ABG∽△DEG
∴$\frac {AG}{DG}=\frac {AB}{DE}=2$
∴$\frac {AG}{AD}=\frac 23$