2026年同步练习江苏九年级数学下册苏科版第134页解析答案

24. (10分)如图,有一段长$400\ \mathrm{m}$的海堤,其横截面是梯形$ABCD$,为了提高防海潮的能力,计划将堤面加宽$1.6\ \mathrm{m}$,背水坡的坡度由原来的$1:1$改成$1:2$,加固后的海堤横截面是梯形$BCEF$. 已知原背水坡$AD$的长为$8.0\ \mathrm{m}$,求完成这一工程所需的土方(精确到$1\ \mathrm{m}^3$).

答案：
解：过点D作DM⊥AB，垂足为点M，过点E作EN⊥BF，垂足为点N

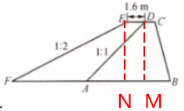
由题意可得，DM=EN，DE=MN=1.6m
在Rt△ADM中，∵AD=8，坡度i=tan∠DAM=DM：AM=1：1
∴∠DAM=45°
∴$DM=AM=\frac {AD}{\sqrt 2}=4\sqrt 2$
∴$EN=DM=4\sqrt 2$
在Rt△EFN中，∵坡度i=EN：FN=1：2
∴$FN=8\sqrt 2$
∴$FA=FN+MN-AM=4\sqrt 2+1.6$
∴$S_{梯形DEFA}=\frac 12(DE+AF)×EN=16+6.4\sqrt 2$
$400(16+6.4\sqrt 2)=6400+2560\sqrt 2≈10020(\ \mathrm {m^3})$
∴完成这一工程所需的土方约为$10020\ \mathrm {m^3}$

25. (10分)如图,$AC$是某市环城路的一段,$AE$、$BF$、$CD$都是南北方向的街道,其与环城路$AC$的交叉路口分别是点$A$、$B$、$C$. 已知花卉世界$D$位于点$A$的北偏东$45^{\circ}$方向和点$B$的北偏东$30^{\circ}$方向上,$AB = 2\ \mathrm{km}$,$\angle DAC = 15^{\circ}$. 分别求交叉路口$B$、$C$与花卉世界$D$的距离.

答案：
解：由题意，得∠EAD=45°，∠FBD=30°
∴∠EAC=∠EAD+∠DAC=45°+15°=60°
∵AE//BF//CD
∴∠FBC=∠EAC=60°
∴∠DBC=30°
∵∠DBC=∠DAB+∠ADB
∴∠ADB=15°
∴∠DAB=∠ADB
∴BD=AB=2
过点B作BO⊥DC，交其延长线于点O

在Rt△DBO中，BD=2，∠DBO=60°
∴$DO=2× s in 60°=2× \frac {\sqrt{3}}{2}=\sqrt{3}，$BO=2× cos 60°=1
在 Rt △CBO中，∠CBO=30°，$CO=BOtan 30°=\frac {\sqrt{3}}{3}$
∴$CD=DO-CO=\sqrt 3- \frac {\sqrt{3}}{3}=\frac {2\sqrt{3}}{3}$
路口B、C与花卉世界D的距离分别为$2\ \mathrm {km}、$$\frac {2\sqrt{3}}{3}\ \mathrm {km}$

26. (10分)如图,一架飞机在空中的$A$处,测得下方两个山头$C$、$D$的俯角分别为$60^{\circ}$和$30^{\circ}$,飞机从$A$处沿水平方向飞行$6\ \mathrm{km}$到达山头$D$正上方的点$B$处(点$A$、$B$、$C$、$D$在同一平面内),此时测得山头$C$的俯角为$30^{\circ}$. 求山头$C$、$D$之间的距离.

答案：
解：在Rt△ABD中，∵∠BAD=30°
∴$BD=AB · tan 30°=6× \frac {\sqrt{3}}{3}=2 \sqrt{3}$
∵∠BAC=60°，∠ABC=30°
∴∠ACB=90°
∴$BC=AB · cos 30°=6× \frac {\sqrt{3}}{2}=3 \sqrt{3}$
过点C作CE⊥BD，垂足为E

则∠CBE=60°，$CE=BC · s in 60°=\frac {9}{2}$
∴$BE=BC · cos 60°=\frac {3\sqrt{3}}{2}，$$DE=BD-BE=2 \sqrt{3} - \frac {3\sqrt{3}}{2}=\frac {\sqrt{3}}{2}$
∴在Rt△CDE中，$CD=\sqrt{CE^2+DE^2}=\sqrt{(\frac {9}{2})^2+(\frac {\sqrt{3}}{2})^2}=\sqrt{21}$
∴两山头之间的距离为$ \sqrt{21}\ \mathrm {km}$