2. 如图,在$ □ ABCD $中,$ DE ⊥ AB $,垂足为$ E $,$ AB : BC = 6 : 5 $,$ □ ABCD $的周长为$ 110 $,面积为$ 600 $. 求$ \cos \angle EDA $的值.

答案:解:∵AB∶BC=6∶5,▱ABCD的周长为110
∴$AB=110÷2×\frac {6}{6+5}=30,$$BC=110÷2×\frac 5{6+5}=25$
∵$S_{▱ABCD}=AB×DE=600$
∴DE=20
在Rt△ADE中,∵AD=BC=25,DE=20
∴$cos∠EDA=\frac {DE}{AD}=\frac{4}5$
3. 已知$ \triangle ABC $的三边$ a、b、c $满足$ a^2 + b^2 + c^2 = ab + ac + bc $. 试判断$ \triangle ABC $的形状.
答案:解:∵$a^2+b^2+c^2=ab+ac+bc$
∴$2a^2+2b^2+2c^2=2ab+2ac+2bc,$即$(a-b)^2+(b-c)^2+(a-c)^2=0$
∴a-b=0,b-c=0,a-c=0,即a=b=c
∴△ABC为等边三角形
4. 如图,圆柱形容器的高为$ 1.2 $m,底面周长为$ 1 $m,在容器内壁离容器底部$ 0.3 $m的点$ B $处有一蚊子,此时一只壁虎正好在容器外壁离容器上沿$ 0.3 $m且与蚊子相对的点$ A $处. 壁虎捕捉蚊子的最短路线长为
1.3
m. (容器厚度忽略不计)

答案:1.3
5. 在四边形$ ABCD $中,$ \angle ABC = 60^{\circ} $,$ AC $平分$ \angle BAD $,$ AC = 7 $,$ AD = 6 $,$ S_{\triangle ADC} = \dfrac{15}{2} \sqrt{3} $. 求$ BC $和$ AB $的长.

答案:解:过点C作CE⊥AD,垂足为点E,
作CF⊥AB,垂足为点F
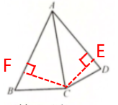
∵AD=6,$S_{△ABC}=\frac 12×AD×CE=\frac {15\sqrt 3}2$
∴$CE=\frac {5\sqrt 3}2$
∵AC平分∠BAD
∴$CF=CE=\frac {5\sqrt 3}2$
在Rt△BCF 中,∵$CF=\frac {5\sqrt 3}2,$∠ABC=60°
∴$BF=\frac {CF}{\sqrt 3}=\frac 52,$BC=2BF=5
在Rt△ACF 中,∵$CF=\frac {5\sqrt 3}2,$AC=7
∴$AF=\sqrt {AC^2-CF^2}=\frac {11}{2}$
∴$AB=AF+BF=\frac {11}{2}+\frac {5}{2}=8$
综上所述,BC=5,AB=8
6. 如图①、②、③中,$ E、D $分别是正三角形$ ABC $、正四边形$ ABCM $、正五边形$ ABCMN $中$ \angle C $的两边上的点,且$ BE = CD $,$ DB $与$ AE $相交于点$ P $.
(1) 求图①中$ \angle APD $的度数.
(2) 图②中,$ \angle APD $的度数为
90°
,图③中,$ \angle APD $的度数为
108°
.
(3) 根据前面探索,你能否将本题推广到一般的正$ n $边形情况?若能,写出问题和结论;若不能,请说明理由.

答案:90°
108°
解:(1)∵△ABC为正三角形
∴AB=BC,∠ABE=∠BCD=60°
在△ABE和△BCD中
$\begin{cases}{AB=BC}\\{∠ABE=∠BCD}\\{BE=CD}\end{cases}$
∴$△ABE≌△BCD(\mathrm {SAS})$
∴∠BAE=∠CBD
∴∠APD=∠BAE+∠ABD=∠CBD+∠ABD=∠ABC=60°
(3)能,问题:点E、D分别在正n边形中以点C为顶点的相邻两边上
且BF=CD,DB与AE相交于点P,求∠APD的度数
结论:∠APD的度数为$\frac {(n-2) · 180°}{n}$