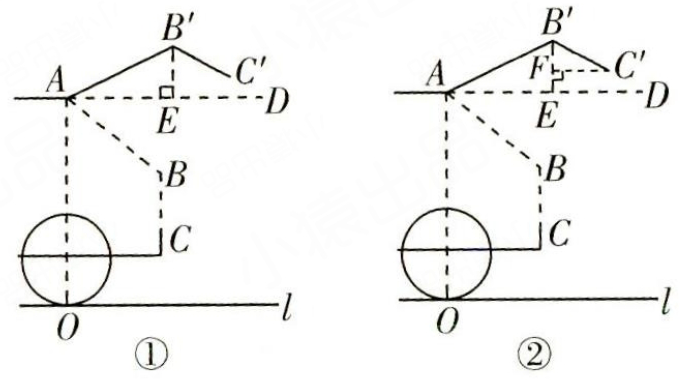
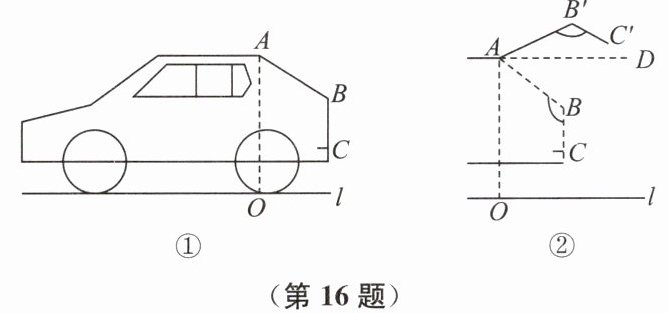
16. (10分)图①是某越野车的侧面示意图,折线段ABC表示车后盖,已知AB=1m,BC=0.6m,∠ABC=123°,该车的高度AO=1.7m。如图②,打开后备箱,车后盖ABC落在AB'C'处,AB'与水平面的夹角∠B'AD=27°。
(1)求打开后备箱后,车后盖最高点B'到地面l的距离。
(2)若小琳爸爸的身高为1.8m,他从打开的车后盖C'处经过,有没有碰头的危险?请说明理由。(精确到0.01m;参考数据:$\sin27^{\circ}\approx0.454$,$\cos27^{\circ}\approx0.891$,$\tan27^{\circ}\approx0.510$,$\sqrt{3}\approx1.732$)
答案:解:(1)如图①,作B'E⊥AD,垂足为E.
在Rt△AB'E中,
因为∠B'AD=27°,
$AB'=AB=1\ \mathrm {m}$
所以$sin 27°=\frac {B'E}{AB'}$
所以$B'E=AB'sin 27°≈1×0.454=0. 454(\mathrm {m}).$
因为平行线间的距离处处相等,
所以$B'E+AO=0.454+1.7=2.154≈2.15(\mathrm {m}).$
答:车后盖最高点B'到地面l的距离约为$2.15\ \mathrm {m}.$
(2)没有碰头的危险,理由如下:
如图②,过点C作C'F⊥B'E.垂足为F.
因为∠B'AD=27°,∠B'EA =90°,
所以∠AB'E = 63°.
因为∠AB'C'=∠ABC= 123°,
所以∠C'B'F=∠AB'C'-∠AB'E = 60°.
在Rt△B'FC'中,$B'C'= BC=0.6\ \mathrm {m}. .$
所以$B'F=B'C'×cos 60° = 0.3(\mathrm {m}).$
因为平行线间的距离处处相等,.
所以点C到地面的距离为$2. 15-0.3= 1.85(\mathrm {m}).$
因为$1.85\gt 1.8.$
所以没有碰头的危险.