1. 直角三角形的性质：直角三角形的两个锐角___________.直角三角形可以用符号“_______”表示，直角三角形ABC可以写成___________.数学语言：若△ABC是直角三角形，且∠C=90°，则∠A+∠B=_______.
2. 直角三角形的判定：有两个角___________的三角形是直角三角形.数学语言：在△ABC中，若∠A+∠B=90°，则△ABC是___________三角形.
答案：1. 互余 Rt△ Rt△ABC 90°
2. 互余 直角
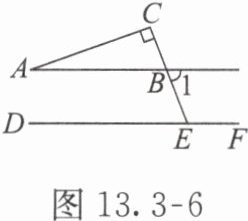
【例1】如图13.3-6，AB//DF，AC⊥BC，垂足为C，CB的延长线与DF相交于点E.若∠A=20°，则∠CEF=（ ）.
A. 70° B. 80° C. 100° D. 110°
答案：D
因为AC⊥BC，所以△ABC是直角三角形，∠ABC=90° - ∠A=90° - 20°=70°.因为AB//DF，所以∠1=∠ABC=70°（∠1为∠BED）.所以∠CEF=180° - ∠1=180° - 70°=110°.
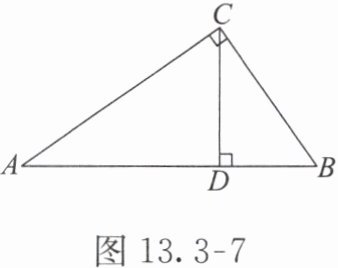
跟踪练习1 如图13.3-7，CD是△ABC的高，∠ACB=90°.若∠A=35°，则∠BCD=（ ）.
A. 25° B. 35° C. 40° D. 45°
答案：B
因为∠ACB=90°，∠A=35°，所以∠B=90° - 35°=55°.因为CD是高，所以∠CDB=90°，则∠BCD=90° - ∠B=90° - 55°=35°.
【例2】在下列条件中，不能判定△ABC是直角三角形的是（ ）.
A. ∠A=∠B - ∠C
B. ∠A=90° - ∠C
C. ∠A=∠B=$\frac{1}{2}$∠C
D. ∠A=2∠B=3∠C
答案：D
A. ∠A+∠C=∠B，∠A+∠B+∠C=180°，则2∠B=180°，∠B=90°，是直角三角形.
B. ∠A+∠C=90°，则∠B=90°，是直角三角形.
C. 设∠A=∠B=x，∠C=2x，x+x+2x=180°，x=45°，∠C=90°，是直角三角形.
D. 设∠A=x，$∠B=\frac{x}{2}，$$∠C=\frac{x}{3}，$$x+\frac{x}{2}+\frac{x}{3}=180°，$$x=\frac{1080°}{11}\gt90°，$不是直角三角形.
