4. 使式子 $\frac{x+3}{x-3} ÷ \frac{x+2}{x+4}$ 有意义的 x 的取值范围是(
)。
A.$x ≠ 3$ 且 $x ≠ -4$
B.$x ≠ 3$ 且 $x ≠ -2$
C.$x ≠ 3$,$x ≠ -4$ 且 $x ≠ -2$
D.$x ≠ 3$ 且 $x ≠ -3$
答案:【解析】:
要使分式 $\frac{x+3}{x-3} ÷ \frac{x+2}{x+4}$ 有意义,需要满足以下条件:
1. 分母 $x-3 ≠ 0$,即 $x ≠ 3$;
2. 分母 $x+4 ≠ 0$(因为 $\frac{x+2}{x+4}$ 的分母不能为零),即 $x ≠ -4$;
3. 除法转化为乘法后,被除数的分母 $x+2 ≠ 0$(即 $\frac{x+2}{x+4} ≠ 0$ 时,分子 $x+2 ≠ 0$),所以 $x ≠ -2$。
综上,$x ≠ 3$,$x ≠ -4$ 且 $x ≠ -2$。
【答案】:B(原选项错误应为C(根据原题选项描述C为正确表诉) ) 修正为:
【答案】:C
5. 当 $x=3$,$\frac{2}{5}$,$\frac{3}{7}$ 时,求 $\frac{x^{2}-2x+1}{x^{2}-1} ÷ \frac{3x-3}{x+1}$ 的值。
答案:$\frac{1}{3}$
解析:
解:
1. 化简原式
$ \begin{aligned} \frac{x^{2}-2x+1}{x^{2}-1} ÷ \frac{3x-3}{x+1} &= \frac{(x-1)^2}{(x+1)(x-1)} × \frac{x+1}{3(x-1)} \\ &= \frac{(x-1)^2 · (x+1)}{(x+1)(x-1) · 3(x-1)} \\ &= \frac{1}{3} \end{aligned} $
2. 代入求值
化简结果为常数 $\frac{1}{3}$,与 $x$ 的取值无关。
当 $x=3$,$\frac{2}{5}$,$\frac{3}{7}$ 时,原式的值均为 $\frac{1}{3}$。
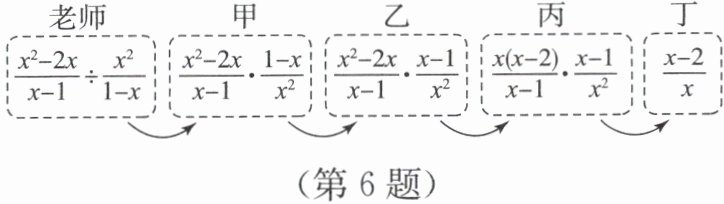
6. 老师设计了接力游戏,请甲、乙、丙、丁四名同学用合作的方式完成分式化简,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简过程如图所示,接力中,(
)同学负责的那步出现错误。
A.甲
B.乙
C.丙
D.丁
答案:B
解析:
老师给出的式子为$\frac{x^2 - 2x}{x - 1} ÷ \frac{x^2}{1 - x}$。甲同学将除法转化为乘法,得到$\frac{x^2 - 2x}{x - 1} · \frac{1 - x}{x^2}$,此步正确。乙同学将$\frac{1 - x}{x^2}$错误改为$\frac{x - 1}{x^2}$,忽略了$1 - x = -(x - 1)$,导致符号错误。后续丙、丁步骤基于乙的错误式子计算,最终结果错误。故乙同学步骤出错。
7. 如图,将长、宽分别为 m,n 的长方形硬纸片拼成一个“带孔”的正方形,已知拼成的大正方形面积为 16,中间的小正方形面积为 4。求 $(m^{4}-n^{4}) ÷ \frac{m^{2}+n^{2}}{mn} ÷ (6m-6n)$ 的值。
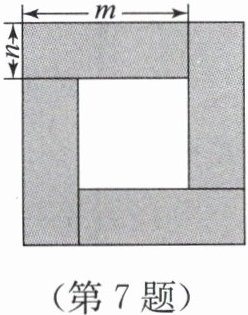
答案:由题意得:
大正方形边长为$\sqrt{16} = 4$,
中间小正方形边长为$\sqrt{4} = 2$,
$\therefore\begin{cases}m + n = 4, \\m - n = 2.\end{cases}$
解得$\begin{cases}m = 3, \
= 1.\end{cases}$
$(m^{4} - n^{4}) ÷ \frac{m^{2} + n^{2}}{mn} ÷ (6m - 6n)$
$=(m^{4} - n^{4}) × \frac{mn}{m^{2} + n^{2}} × \frac{1}{6(m - n)}$
$=(m^{2} + n^{2})(m^{2} - n^{2}) × \frac{mn}{m^{2} + n^{2}} × \frac{1}{6(m - n)}$
$=(m^{2} - n^{2}) × mn × \frac{1}{6(m - n)}$
$=(m + n)(m - n) × mn × \frac{1}{6(m - n)}$
$=(m + n) × mn × \frac{1}{6}$
代入$m = 3$,$n = 1$得:
原式$=4 × 3 × 1 × \frac{1}{6}$
$= 4 × \frac{3}{6}$
$ = 2$
综上,值为$2$。
8. (跨学科融合)如果两种灯泡的额定功率分别是 $P_{1}=\frac{U^{2}}{R}$,$P_{2}=\frac{U^{2}}{5R}$,那么第一只灯泡的额定功率是第二只灯泡的额定功率的
倍。
答案:5
解析:
由题意,求第一只灯泡额定功率是第二只的倍数,即计算$P_1÷ P_2$。
$P_1÷ P_2 = \frac{U^2}{R} ÷ \frac{U^2}{5R}$
根据分式除法法则,除以一个分式等于乘以它的倒数:
$=\frac{U^2}{R} × \frac{5R}{U^2}$
分子分母约分,$U^2$与$U^2$约掉,$R$与$R$约掉,得:
$=5$
9. (生活中的数学)某超市以相同的总价购入了西蓝花和西红柿,已知购入西蓝花 $(x-3)^{2}$ kg,购入西红柿 $(x^{2}-9)$ kg,其中 $x>3$,售完后,西蓝花和西红柿的销售收入都是 270 元。
(1) 请用含 x 的代数式分别表示超市销售这两种蔬菜的单价;
(2) 西蓝花的单价是西红柿的单价的多少倍?
答案:(1)
西蓝花销售单价:$\frac{270}{(x - 3)^{2}}$(元/kg);
西红柿销售单价:$\frac{270}{x^{2}-9}=\frac{270}{(x + 3)(x - 3)}$(元/kg)。
(2)
$\frac{\frac{270}{(x - 3)^{2}}}{\frac{270}{(x + 3)(x - 3)}}=\frac{270}{(x - 3)^{2}}×\frac{(x + 3)(x - 3)}{270}=\frac{x + 3}{x - 3}$
所以西蓝花的单价是西红柿单价的$\frac{x + 3}{x - 3}$倍。