6. 计算：
（1）$(3a^{2}b)^{3}(-2ab^{2})^{2}÷ (6a^{5}b^{3})$；
（2）$(7x^{3}y^{2})÷ [(-7x^{5}y^{5})÷ (-\frac{1}{3}x^{3}y^{2})]$.
答案：（1）$18a^{3}b^{4}$
解析：$(3a^{2}b)^{3}(-2ab^{2})^{2}÷ (6a^{5}b^{3})$
$=27a^{6}b^{3}×4a^{2}b^{4}÷ (6a^{5}b^{3})$
$=108a^{8}b^{7}÷ (6a^{5}b^{3})$
$=18a^{3}b^{4}$
（2）$\frac{1}{3}y^{-1}$
解析：$(7x^{3}y^{2})÷ [(-7x^{5}y^{5})÷ (-\frac{1}{3}x^{3}y^{2})]$
$=7x^{3}y^{2}÷ (21x^{2}y^{3})$
$=\frac{1}{3}x^{3 - 2}y^{2 - 3}$
$=\frac{1}{3}xy^{-1}$？
解析：$(-7x^5y^5)÷(-\frac{1}{3}x^3y^2)=21x^{2}y^{3}$，$7x^3y^2÷21x^2y^3=\frac{1}{3}xy^{-1}=\frac{x}{3y}$
7. 小亮在计算$(6x^{3}y - 3x^{2}y^{2})÷ (3xy)$时，错把多项式的减号写成了加号，那么正确结果与错误结果的乘积是（ ）.
A. $2x^{2}-xy$
B. $2x^{2}+xy$
C. $4x^{4}+x^{2}y^{2}$
D. $4x^{4}-x^{2}y^{2}$
答案：D
解析：正确结果：$(6x^{3}y - 3x^{2}y^{2})÷ (3xy)=2x^{2}-xy$
错误结果：$(6x^{3}y + 3x^{2}y^{2})÷ (3xy)=2x^{2}+xy$
乘积：$(2x^{2}-xy)(2x^{2}+xy)=4x^{4}-x^{2}y^{2}$
8. 已知M，N均为整式，$M=(xy + 1)(xy - 2)-2x^{2}y^{2}+2$，小刚在计算$M÷ N$时，误把“÷”抄成了“-”，这样他计算的结果为$-x^{2}y^{2}$.
（1）将整式M化为最简形式；
（2）求$M÷ N$的正确结果.
答案：（1）$-x^{2}y^{2}-xy$
解析：$M=(xy + 1)(xy - 2)-2x^{2}y^{2}+2$
$=x^{2}y^{2}-2xy + xy - 2 - 2x^{2}y^{2}+2$
$=-x^{2}y^{2}-xy$
（2）$xy + 1$
解析：因为$M - N=-x^{2}y^{2}$，所以$N = M + x^{2}y^{2}=-x^{2}y^{2}-xy + x^{2}y^{2}=-xy$
则$M÷ N=(-x^{2}y^{2}-xy)÷ (-xy)=xy + 1$
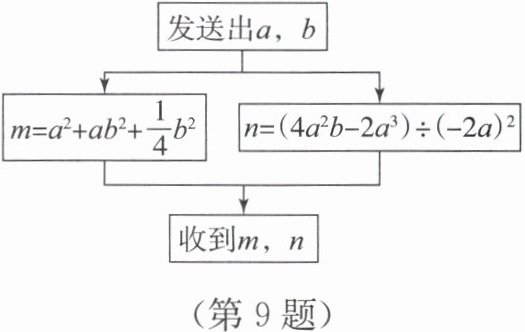
9. （创新考法）信息时代确保信息的安全很重要，于是在传输信息的时候需要加密传输，发送方将明文加密为密文传输给接收方，接收方收到密文后解密还原为明文.已知某种加密规则如图所示，当发送方发送出$a = 1$，$b = 2$时，接收方收到的密文之积$mn=$_______.
发送出$a,b$→$m = a^{2}+ab+\frac{1}{4}b^{2}$，$n=(4a^{2}b - 2a)÷ (-2a)$→收到$m,n$
（第9题）
答案：-15
解析：当$a = 1$，$b = 2$时，
$m = 1^{2}+1×2+\frac{1}{4}×2^{2}=1 + 2 + 1=4$
$n=(4×1^{2}×2 - 2×1)÷ (-2×1)=(8 - 2)÷ (-2)=6÷ (-2)=-3$
则$mn=4×(-3)=-12$？
解析：$m = a^2 + ab + \frac{1}{4}b^2=(a + \frac{b}{2})^2=(1 + 1)^2=4$，$n=(4a^2b - 2a)÷(-2a)=-2ab + 1=-2×1×2 + 1=-3$，$mn=4×(-3)=-12$
10. （数学思想方法）【阅读材料】由两个或两类对象在某些方面的相同或相似，得出它们在其他方面也可能相同或相似的推理方法叫作类比法.多项式除以多项式可以类比多位数的除法进行计算.
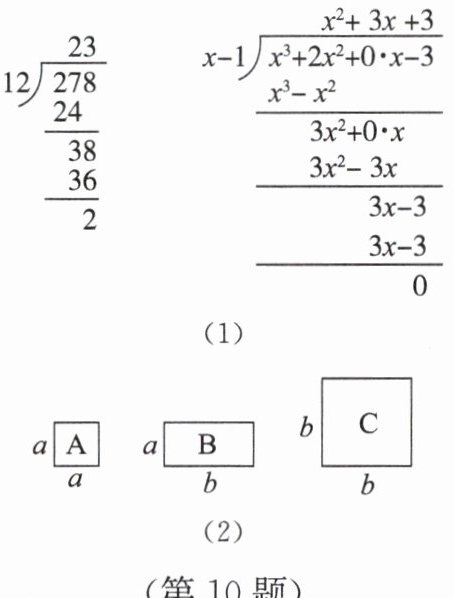
如图（1），可得
$278÷12 = 23·s·s2$，
$(x^{3}+2x^{2}-3)÷(x - 1)=x^{2}+3x + 3$.
即多项式除以多项式用竖式计算，步骤如下：
①把被除式和除式按同一字母的指数从大到小依次排列（若有缺项用零补齐）；
②用竖式进行运算；
③当余式的次数低于除式的次数时，运算终止，得到商式和余式.若余式为零，说明被除式能被除式整除.
例如：$(x^{3}+2x^{2}-3)÷(x - 1)=x^{2}+3x + 3$，因为余式为0，所以$x^{3}+2x^{2}-3$能被$x - 1$整除.
（1）$(x^{2}+7x + 6)÷(x + 1)=$_______.
答案：$x + 6$
解析：用竖式计算：
```
x + 6
____________
x + 1 | x² + 7x + 6
x² + x
-------
6x + 6
6x + 6
-------
0
```
所以商式为$x + 6$，余式为0。
