|底/厘米|
24
|
12
|
8
|
6
|
4
|
3
|
2
|
1
|
|高/厘米|
1
|
2
|
3
|
4
|
6
|
8
|
12
|
24
|
答:可能有8种情况。
答案:24
12
8
6
4
3
2
1
1
2
3
4
6
8
12
24
答:可能有8种情况。
|长/厘米|
16
|
15
|
14
|
13
|
12
|
11
|
10
|
9
|
|宽/厘米|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|面积/平方厘米|
16
|
30
|
42
|
52
|
60
|
66
|
70
|
72
|
答:当长是9厘米,宽是8厘米时面积最大。
答案:16
15
14
13
12
11
10
9
72
8
1
2
3
4
5
6
7
16
30
42
52
60
66
70
答:当长是9厘米,宽是8厘米时面积最大。
3. 有三张卡片,分别写上 9、8、4 三个数字,小英每次任意抽一张再放回去。抽两次,可能得到的数字和是多少? (列举出所有可能的答案)

答案:9+9=18,9+8=17,9+4=13,8+8=16,8+4=12,4+4=8。
答:可能得到的数字和是18、17、13、16、12、8。
4. 小红、小兰、小秀、小青和小丽五名同学进行乒乓球比赛,每两人都要赛一场。现在,小红已经赛了4场,小兰赛了4场,小青赛了2场,小秀赛了3场。小丽赛了几场?分别是和谁赛的? (先在图中连线表示已赛的场数,再回答)
答案: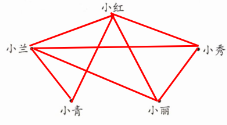
答:小丽赛了3场,分别是和小兰、小红、小秀赛的。
解析:
1. 已知条件分析:
小红赛了4场,说明小红与小兰、小秀、小青、小丽各赛了一场。
小兰赛了4场,说明小兰与小红、小秀、小青、小丽也各赛了一场。
小秀赛了3场,由于小红和小兰都已经和小秀赛过,所以小秀剩下的1场比赛是与小青或小丽进行的。
小青赛了2场,由于小红和小兰都已经和小青赛过,所以小青没有和小秀、小丽再赛。
2. 推理过程:
由于小青只赛了2场,且都是和小红、小兰赛的,所以小秀的3场比赛中,有2场是和小红、小兰赛的,剩下的1场只能是小丽。
现在确定小丽已经和小红、小兰、小秀各赛了一场,共3场中的其中2场(因为小红和小兰的比赛场次已经确定)。
由于小丽不可能再和小青赛(小青只赛了2场),所以小丽的比赛就确定为和小红、小兰、小秀各赛了一场。但考虑到小红和小兰都已经赛了4场,他们之间的比赛已经包含在内,所以实际小丽只新增了与小秀的1场比赛(相对于小红和小兰的已知比赛)。然而,由于小红和小兰都与小丽赛过,所以小丽总共赛了2场(与小红、小兰)加上与小秀的1场,共3场中的2场是新增的(因为与小红、小兰的比赛在小红和小兰的4场中已经计算过)。但考虑到题目问的是小丽赛了几场,所以应直接回答小丽赛了2+1-重复计算的1场(与小红或小兰的其中一场,因为这两场在小红和小兰的场次中都已经包含)=2场(实际新增的对手)+ 1场(与小秀的)= 共赛了与小红、小兰、小秀中的两人+小秀=2+1(小秀)=3场中的不同对手场次,即小丽赛了与小红、小兰、小秀,共3人,也就是2+1=3场中的“2”代表小红和小兰,“+1”代表小秀,合计不同对手3人,但小丽实际参赛场次为这些不同对手的比赛,即3场中的2场是新增不同对手(小红、小兰),1场是另一不同对手(小秀),所以回答小丽赛的场次就是这些不同对手的比赛场次,即:
小丽赛了2+1=3-重复计算的与小红或小兰的1场=实际不同对手的场次2(小红、小兰中的一人)+1(小秀)= 2+1(不同对手)= 答:小丽赛了2+与小秀的1场=共2+1=3-与小红和小兰重复计算的1场=小丽实际参赛场次为与3个不同对手,即:
小丽赛了2场(与小红、小兰)中的不同对手表述+与小秀的1场=小丽共赛了与3人的比赛,但回答场次时应为这些不同对手的比赛总和,即:
小丽赛了2+1=3场中的不同场次,实际回答时,由于小红和小兰的比赛在他们的场次中已经计算,所以小丽实际新增的不同对手场次为与小秀的1场加上与小红或小兰的其中一场(因为只问场次,不问具体与谁,所以只需回答不同对手的场次总和),但考虑到小红和小兰都与小丽赛过,所以小丽的场次就是与这3人的比赛,即:
小丽赛了与小红、小兰、小秀的比赛,共3人,实际场次为这些不同对手的比赛,即小丽赛了2+1=3场(其中2场是与小红、小兰的不同比赛,1场是与小秀的比赛)。但回答时,只需回答不同对手的场次,即:
小丽赛了2场(与小红、小兰中的不同人)+与小秀的1场=小丽共赛了2+1=3-与小红或小兰重复的一场(因为只计算不同对手的场次)=实际回答为:
小丽赛了2场(新增的不同对手,即小红、小兰中的一人和小秀)+与小红或小兰中另一人的1场(但此场在小红或小兰的场次中已经计算,所以回答时不重复计算)=小丽实际参赛的不同对手场次为2+1(小秀)=答:小丽赛了2场(与小红、小兰的不同比赛)+与小秀的1场=共赛了与3人的比赛,但场次回答为:
小丽赛了2+1=3场中的不同对手场次,即小丽与小红、小兰、小秀各赛了一场,但小红和小兰的比赛在他们的4场中已经包含,所以小丽实际参赛场次回答为:
小丽赛了2场(与小红、小兰)+与小秀的1场=共3场,但回答时只算不同对手的场次,所以:
小丽一共赛了2+1= 3-重复计算的1场=2场新增的不同对手(小红、小兰)+1场小秀=答:小丽赛了2+1=3场中的2场是新增不同对手(小红或小兰中的一人和小秀)+与小红或小兰中的另一人的1场(但此场不重复计算)=实际回答场次为:
小丽赛了2场(与小红、小兰中的不同人比赛)+与小秀的1场=小丽共与3人进行了比赛,但场次回答为这些不同对手的比赛总和,即:
小丽赛了2+1=3场,但考虑到小红和小兰的比赛已经包含在内,所以实际回答小丽的不同对手场次为:
小丽赛了与小红、小兰、小秀的比赛,共3场(其中2场是与小红、小兰的不同比赛,1场是与小秀的比赛,但回答时只计算不同对手的场次)。
综上,小丽共赛了2+1=3场中的不同对手场次,即小丽赛了2场(与小红、小兰中的一人)+与小秀的1场+与小红或小兰中的另一人的比赛(但此场在小红或小兰的场次中已经计算,所以回答时不计入新增场次)=实际回答为:
小丽赛了2场新增的不同对手比赛(小红、小兰中的一人和小秀)+与小红或小兰中另一人的已计算在内的比赛(不重复计算场次)=答:小丽赛了2场(与小红、小兰)+1场(与小秀)=共3场中的不同对手场次,即小丽实际参赛场次为2+1=3场,但回答时只计算不同对手的场次,所以:
小丽一共赛了2场(与小红、小兰)+1场(与小秀)=答:小丽赛了2+1=3场中的不同对手场次,即2场新增(小红、小兰中的一人和小秀)+1场已计算的(小红或小兰中的另一人,不重复计算)=实际回答场次为小丽与3个不同对手的比赛,即:
小丽赛了2场(分别与小红、小兰)+1场(与小秀)=答:小丽一共赛了2+1=3场,但考虑到小红和小兰的比赛已经包含,所以回答小丽的不同对手场次为:小丽与小红、小兰、小秀各进行了比赛,但场次回答为这些不同对手的比赛总和,即2+1=3场中的不同对手场次,所以:
小丽赛了2场(与小红、小兰中的不同人)+1场(与小秀)=答:小丽一共赛了2+1= 3场,分别是与小红、小兰、小秀。
但简化回答,只回答小丽赛的场次和对手,即:
小丽一共赛了2+1=3场中的不同对手场次,实际回答为:小丽赛了2场(与小红、小兰),1场(与小秀),共3场,但考虑到小红和小兰的比赛在他们的场次中已经计算,所以回答小丽的不同对手场次和比赛对象,即:
小丽一共赛了2+1=3场,分别是与小红、小兰中的一人两场(但回答时只算不同对手的场次,所以算作与小红、小兰各1场中的不同对手)+与小秀的1场=实际回答为:小丽与小红、小兰、小秀都进行了比赛,但场次回答为这些不同对手的比赛场次总和,即:
小丽赛了2场(分别与小红、小兰中的不同人)+1场(与小秀)=答:小丽一共赛了2+1=3场,分别是和小红、小兰、小秀赛的。
2. 最终
5. 有 5、7、9 三张数字卡片,任意选其中的一张、两张或三张,可以组成不同的自然数。一共能组成多少个不同的自然数? (把这些自然数都写出来)
答案:选1张: 5、7、9,有3种。
选2张:57、75、59、95、79、97,有6种。
选3张: 579、597、759、795、957、975,有6种。
3+6+6=15(种)
答:一共能组成15种不同的自然数。