25. (9 分)如图所示,滑动变阻器标有“$ 50\ \Omega $,$ 1\ A $”字样,电源电压为 $ 18\ V $ 恒定不变。当开关 $ S $ 闭合后,电流表示数为 $ 0.5\ A $,电压表示数为 $ 5\ V $。求:
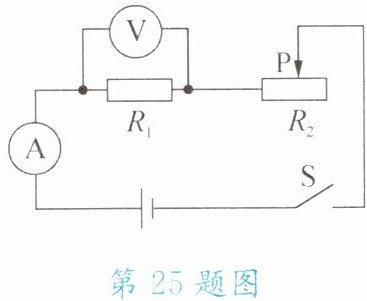
(1)电阻 $ R_1 $ 的阻值。
(2)这时滑动变阻器连入电路的有效电阻值。
(3)若电流表量程为 $ 0\sim 0.6\ A $,电压表量程为 $ 0\sim 15\ V $,则滑动变阻器连入电路的有效阻值不能小于多少欧姆?
答案:(1)10Ω (2)26Ω (3)20Ω
解析:
(1)由电路图可知,$R_1$与$R_2$串联,电压表测$R_1$两端电压,电流表测电路电流。已知$U_1 = 5\ V$,$I = 0.5\ A$,根据$I=\frac{U}{R}$,$R_1=\frac{U_1}{I}=\frac{5\ V}{0.5\ A} = 10\ \Omega$。
(2)电源电压$U = 18\ V$,$R_2$两端电压$U_2=U - U_1=18\ V-5\ V=13\ V$,则$R_2=\frac{U_2}{I}=\frac{13\ V}{0.5\ A} = 26\ \Omega$。
(3)电流表量程$0 - 0.6\ A$,滑动变阻器允许最大电流$1\ A$,电路最大电流$I_{max}=0.6\ A$。此时$R_1$两端电压$U_{1max}=I_{max}R_1=0.6\ A×10\ \Omega = 6\ V<15\ V$(电压表安全)。总电阻$R_{总min}=\frac{U}{I_{max}}=\frac{18\ V}{0.6\ A} = 30\ \Omega$,滑动变阻器最小阻值$R_{2min}=R_{总min}-R_1=30\ \Omega - 10\ \Omega=20\ \Omega$。
26. 研究表明,有些金属电阻的阻值会随温度的变化而变化,利用这类金属的特性可以制成金属电阻温度计,它可以用来测量很高的温度,其原理如图所示。图中电流表的量程为 $ 0\sim 15\ mA $(电阻可忽略不计),电源的电压恒为 $ 3\ V $,$ R' $ 为滑动变阻器。金属电阻作为温度计的测温探头,在 $ t\geqslant 0\ °C $ 时,其阻值 $ R_t $ 随温度 $ t $ 的变化关系为 $ R_t = 100 + 0.5t $(单位为欧姆)。

(1)若要把 $ R_t $ 放入温度为 $ 0\ °C $ 处进行测量,使电流表恰好达到满偏电流 $ 15\ mA $,则这时滑动变阻器 $ R' $ 接入电路的阻值为多大?
(2)保持问题(1)中滑动变阻器 $ R' $ 接入电路的阻值不变,当把测温探头 $ R_t $ 放到某待测温度处时,电流表的示数恰为 $ 10\ mA $,此时 $ R_t $ 的阻值为多大?对应的温度为多高?
(3)若把电流表的电流刻度换为对应的温度刻度,则温度刻度的特点是什么?
答案:解:$(1)R_t=100\ \mathrm {Ω}$
$ R'+100Ω=\frac {U_{ }}{I_{ }}=\frac {{ 3 }\ \text {V}}{{ 0.015 }\ \text {A}}={200 }Ω$
得$R'=100\ \mathrm {Ω}$
$ (2)R_{ t }+100Ω=\frac {U_{ }}{I'}=\frac {{ 3 }\ \text {V}}{{ 0.01 }\ \text {A}}={ 300 }Ω$
得$R_t=200\ \mathrm {Ω}$
由200=100+0.5t,得t=200℃
(3)电流刻度值越小,对应的温度刻度值越大