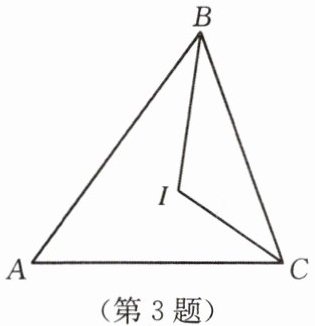
3. 如图,在$\triangle ABC$中,$\angle ABC$,$\angle ACB的平分线交于点I$,则$\angle BIC$的度数是(
A
)
A.$90^{\circ} + \frac{1}{2}\angle A$
B.$90^{\circ} - \frac{1}{2}\angle A$
C.$180^{\circ} - \angle A$
D.$180^{\circ} - \frac{1}{2}\angle A$
]
解析:
证明:在$\triangle ABC$中,$\angle ABC + \angle ACB = 180° - \angle A$。
∵$BI$、$CI$分别平分$\angle ABC$、$\angle ACB$,
∴$\angle IBC = \frac{1}{2}\angle ABC$,$\angle ICB = \frac{1}{2}\angle ACB$。
∴$\angle IBC + \angle ICB = \frac{1}{2}(\angle ABC + \angle ACB) = \frac{1}{2}(180° - \angle A) = 90° - \frac{1}{2}\angle A$。
在$\triangle BIC$中,$\angle BIC = 180° - (\angle IBC + \angle ICB) = 180° - (90° - \frac{1}{2}\angle A) = 90° + \frac{1}{2}\angle A$。
A