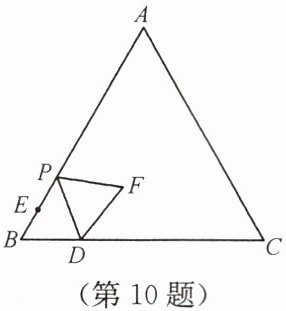
2025年新课程自主学习与测评八年级数学上册人教版第70页解析答案

10. 如图,在等边$\triangle ABC$中,$AB = 10$,$BD = 4$,$BE = 2$,点 $P$ 从点 $E$ 出发沿 $EA$ 方向运动,连接 $PD$,以 $PD$ 为边,在 $PD$ 右侧按如图方式作等边$\triangle DPF$,当点 $P$ 从点 $E$ 运动到点 $A$ 时,点 $F$ 运动的路径长是(

)

A.$8$
B.$10$
C.$3\pi$
D.$5\pi$

答案：A

解析：

证明：连接CF，过F作FQ⊥BC于Q，过P作PH⊥BC于H。
设∠PDB=α，则∠PDF=60°，∠FDQ=120°-α。
在等边△ABC中，∠B=60°，
∴∠BPD=120°-α，
∴∠BPD=∠FDQ。
∵△DPF是等边三角形，
∴PD=FD。
在△PBD和△DQE中，∠PHD=∠FQD=90°，∠BPD=∠FDQ，PD=FD，
∴△PHD≌△DQE(AAS)，
∴DQ=PH，FQ=DH。
设BP=x，BE=2，AB=10，
∴PE=x-2，PH=BP·sin60°= $\frac{\sqrt{3}}{2}x$，BH=BP·cos60°= $\frac{x}{2}$，DH=BD-BH=4- $\frac{x}{2}$。
DQ=PH= $\frac{\sqrt{3}}{2}x$，CQ=BC-BD-DQ=10-4- $\frac{\sqrt{3}}{2}x$=6- $\frac{\sqrt{3}}{2}x$，FQ=DH=4- $\frac{x}{2}$。
点F坐标可表示为(CQ,FQ)=(6- $\frac{\sqrt{3}}{2}x$,4- $\frac{x}{2}$)，设F(x_F,y_F)，则x_F=6- $\frac{\sqrt{3}}{2}x$，y_F=4- $\frac{x}{2}$，消去x得x_F=6- $\sqrt{3}(4-y_F)$，即x_F= $\sqrt{3}y_F$-6 $\sqrt{3}$+6，
∴F点在定直线上运动。
当P=E时，x=2，F1(6- $\sqrt{3}$,3)；当P=A时，x=10，F2(6-5 $\sqrt{3}$,-1)。
F点运动路径长为F1F2的距离：$\sqrt{( (6- $\sqrt{3}$)-(6-5 $\sqrt{3}$) )^2+(3-(-1))^2}$= $\sqrt{(4 $\sqrt{3}$)^2+4^2}$=8。
答案：A

11. 如图,图中共有

个三角形,以$\angle C$ 为一个内角的三角形有

△ABC,△EBC

。

答案：5;△ABC,△EBC.

12. 已知一个等腰三角形的两边长分别是 $2$ 和 $4$,则该等腰三角形的周长等于

。

答案：10

解析：

情况1：若腰长为2，底边长为4，此时2+2=4，不满足三角形两边之和大于第三边，舍去。
情况2：若腰长为4，底边长为2，此时4+2＞4，4+4＞2，满足三角形三边关系。周长为4+4+2=10。
10

13. 一个等腰三角形底边的长为 $5\mathrm{cm}$,一腰上的中线把其周长分成的两部分的差为 $2.5\mathrm{cm}$,则其腰长为

7.5 cm

。

答案：7.5 cm

解析：

设等腰三角形的腰长为$x\mathrm{cm}$，腰上的中线长为$d\mathrm{cm}$。
周长被中线分成的两部分：一部分为$x + \frac{x}{2} = \frac{3x}{2}$，另一部分为$\frac{x}{2} + 5$。
情况一：$\frac{3x}{2} - (\frac{x}{2} + 5) = 2.5$
$\frac{3x}{2} - \frac{x}{2} - 5 = 2.5$
$x - 5 = 2.5$
$x = 7.5$
情况二：$(\frac{x}{2} + 5) - \frac{3x}{2} = 2.5$
$\frac{x}{2} + 5 - \frac{3x}{2} = 2.5$
$-x + 5 = 2.5$
$-x = -2.5$
$x = 2.5$
当$x = 2.5$时，三边长为$2.5\mathrm{cm}, 2.5\mathrm{cm}, 5\mathrm{cm}$，$2.5 + 2.5 = 5$，不满足三角形两边之和大于第三边，舍去。
故腰长为$7.5\mathrm{cm}$。
$7.5\mathrm{cm}$

14. 如果点$(3,b)和(a,2)$关于 $x$ 轴对称,则 $a + b = $

。

答案：1

解析：

关于$x$轴对称的点，横坐标相同，纵坐标互为相反数。
因为点$(3,b)$和$(a,2)$关于$x$轴对称，
所以$a = 3$，$b = -2$。
则$a + b = 3 + (-2) = 1$。
1

15. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$CA = CB$,$AD$ 平分$\angle CAB$,交 $BC$ 于点 $D$,$DE\perp AB$ 于点 $E$,且 $AB = 6$,则$\triangle DEB$ 的周长为

。

答案：6

解析：

证明：
∵ $\angle C = 90°$，$CA = CB$，
∴ $\triangle ABC$ 是等腰直角三角形，$\angle B = 45°$。
∵ $AD$ 平分 $\angle CAB$，$DE \perp AB$，$DC \perp AC$，
∴ $DC = DE$（角平分线性质）。
在 $Rt\triangle ACD$ 和 $Rt\triangle AED$ 中，
$\begin{cases} AD = AD \\ DC = DE \end{cases}$，
∴ $Rt\triangle ACD \cong Rt\triangle AED$（HL），
∴ $AC = AE$。
∵ $AC = CB$，
∴ $CB = AE$。
$\triangle DEB$ 的周长 $= DE + EB + BD$，
∵ $DE = DC$，
∴ 周长 $= DC + EB + BD = (DC + BD) + EB = CB + EB = AE + EB = AB$。
∵ $AB = 6$，
∴ $\triangle DEB$ 的周长为 $6$。
6

16. 如图,$AB = AC$,若要使$\triangle ABE\cong\triangle ACD$,则还需要补充条件

∠B=∠C（不唯一）

。(只需写一个条件即可)

答案：∠B=∠C（不唯一）

17. 如图,在平面镜里看到背后墙上的电子钟示数如图所示,这时的实际时间应该是

21:05

。

答案：21:05

18. 如图,在$\triangle ABC$中,$\angle B = 30^{\circ}$,$BC$ 的垂直平分线交 $AB$ 于点 $E$,垂足为 $D$,$CE$ 平分$\angle ACB$。若 $BE = 2$,则 $AE$ 的长等于

。

答案：1

解析：

证明：
∵DE垂直平分BC，
∴CE=BE=2，∠EDB=90°。
∵∠B=30°，
∴∠BCE=∠B=30°。
∵CE平分∠ACB，
∴∠ACB=2∠BCE=60°。
在△ABC中，∠A=180°-∠B-∠ACB=90°。
在Rt△AEC中，∠ACE=30°，
∴AE=½CE=½×2=1。
1

19. 如图,$D$,$E$ 为$\triangle ABC$两边 $AB$,$AC$ 的中点,将$\triangle ABC$ 沿线段 $DE$ 折叠,使点 $A$ 落在点 $F$ 处,若$\angle B = 55^{\circ}$,则$\angle BDF = $

$^{\circ}$。

答案：70

解析：

证明：
∵D，E为△ABC两边AB，AC的中点，
∴DE是△ABC的中位线，
∴DE//BC，
∴∠ADE=∠B=55°。
由折叠性质得∠FDE=∠ADE=55°，
∵∠BDF+∠FDE+∠ADE=180°，
∴∠BDF=180°-∠FDE-∠ADE=180°-55°-55°=70°。
70

20. 如图,在等边三角形 $ABC$ 中,过点 $C$ 作垂直于 $BC$ 的直线交$\angle ABC$ 的平分线于点 $P$,且 $BP = 5$,则点 $P$ 到边 $AB$ 所在直线的距离为

$\frac{5}{2}$

。

答案：$\frac{5}{2}$

解析：

证明：
∵△ABC是等边三角形，
∴∠ABC=60°。
∵BP平分∠ABC，
∴∠PBC=$\frac{1}{2}$∠ABC=30°。
∵PC⊥BC，
∴∠PCB=90°。
在Rt△PBC中，∠PBC=30°，BP=5，
∴PC=$\frac{1}{2}$BP=$\frac{5}{2}$。
∵角平分线上的点到角两边的距离相等，
∴点P到AB的距离等于点P到BC的距离PC=$\frac{5}{2}$。
$\frac{5}{2}$