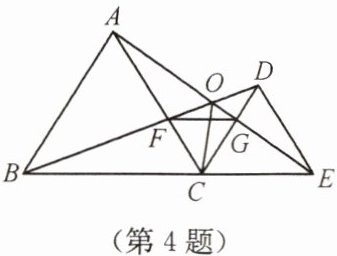
4. 如图,已知$\triangle ABC和\triangle CDE$均是等边三角形,点 $B$,$C$,$E$ 在同一条直线上,$AE$ 与 $BD$ 交于点 $O$,$AE$ 与 $CD$ 交于点 $G$,$BD$ 与 $AC$ 交于点 $F$,连接 $OC$,$FG$,则下列结论:(1)$AE = BD$;(2)$AG = BF$;(3)$\angle BOC = \angle EOC$。其中正确的结论个数是(
D
)
A.$0$ 个
B.$1$ 个
C.$2$ 个
D.$3$ 个
解析:
证明:
(1) $\because \triangle ABC$和$\triangle CDE$均是等边三角形,
$\therefore AC=BC$,$CE=CD$,$\angle ACB=\angle DCE=60°$,
$\therefore \angle ACB+\angle ACD=\angle DCE+\angle ACD$,即$\angle ACE=\angle BCD$,
在$\triangle ACE$和$\triangle BCD$中,
$\left\{\begin{array}{l}AC=BC\\ \angle ACE=\angle BCD\\ CE=CD\end{array}\right.$,
$\therefore \triangle ACE≌\triangle BCD(SAS)$,
$\therefore AE=BD$,故
(1)正确;
(2) $\because \triangle ACE≌\triangle BCD$,
$\therefore \angle CAE=\angle CBD$,
$\because \angle ACB=\angle DCE=60°$,点$B$,$C$,$E$在同一条直线上,
$\therefore \angle ACD=60°$,
在$\triangle AGC$和$\triangle BFC$中,
$\left\{\begin{array}{l}\angle CAE=\angle CBD\\ AC=BC\\ \angle ACG=\angle BCF=60°\end{array}\right.$,
$\therefore \triangle AGC≌\triangle BFC(ASA)$,
$\therefore AG=BF$,故
(2)正确;
(3) 过点$C$作$CM\perp AE$于$M$,$CN\perp BD$于$N$,
$\because \triangle ACE≌\triangle BCD$,
$\therefore S_{\triangle ACE}=S_{\triangle BCD}$,
$\because AE=BD$,
$\therefore CM=CN$,
$\because CM\perp AE$,$CN\perp BD$,
$\therefore OC$平分$\angle AOB$,
$\because \angle AOB=120°$,
$\therefore \angle BOC=\angle EOC=60°$,故
(3)正确。
正确的结论个数是$3$个,答案选D。