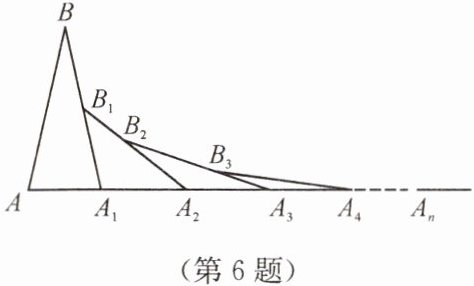
6. 如图,已知 $ AB = A_1B $,$ A_1B_1 = A_1A_2 $,$ A_2B_2 = A_2A_3 $,$ A_3B_3 = A_3A_4 $,…$ $,若 $ \angle A = 70^{\circ} $,则 $ \angle A_n $ 的度数为(
C
)
A.$ \dfrac{70^{\circ}}{2^n} $
B.$ \dfrac{70^{\circ}}{2^{n + 1}} $
C.$ \dfrac{70^{\circ}}{2^{n - 1}} $
D.$ \dfrac{70^{\circ}}{2^{n + 2}} $
解析:
解:在$\triangle ABA_1$中,$AB = A_1B$,$\angle A = 70°$,
$\angle BA_1A=\angle A=70°$,
$\angle BA_1A$是$\triangle A_1B_1A_2$的外角,$A_1B_1 = A_1A_2$,
$\angle A_2A_1B_1=\angle A_1B_1A_2$,
$\angle BA_1A=\angle A_2A_1B_1+\angle A_1B_1A_2=2\angle A_2A_1B_1$,
$\angle A_2A_1B_1=\frac{70°}{2}$,即$\angle A_2=\frac{70°}{2}$。
同理,$\angle A_3=\frac{\angle A_2}{2}=\frac{70°}{2^2}$,
$\angle A_4=\frac{\angle A_3}{2}=\frac{70°}{2^3}$,
……
依此类推,$\angle A_n=\frac{70°}{2^{n-1}}$。
答案:C