2025年新课程自主学习与测评八年级数学上册人教版第50页解析答案

如图,已知△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),现将点B向右平移2个单位长度后再向上平移4个单位长度到达点$B_1,$若设△ABC的面积为$S_1,△AB_1C$的面积为$S_2,$则$S_1,S_2$的大小关系为(

)
A. $S_1＞S_2$
B. $S_1= S_2$
C. $S_1＜S_2$
D. 无法确定

答案：B.

解析：

解：
计算$S_1$：
$A(-4,-3)$，$B(0,-3)$，$AB$在直线$y=-3$上，
$AB$长度：$|0 - (-4)| = 4$，
点$C(-2,1)$到$AB$的距离（$y$坐标差的绝对值）：$|1 - (-3)| = 4$，
$S_1 = \frac{1}{2} × 4 × 4 = 8$。
计算$S_2$：
点$B$平移后得$B_1$：向右2个单位，向上4个单位，
$B_1$坐标：$(0+2, -3+4) = (2,1)$，
$A(-4,-3)$，$C(-2,1)$，$B_1(2,1)$，
$CB_1$在直线$y=1$上，长度：$|2 - (-2)| = 4$，
点$A$到$CB_1$的距离（$y$坐标差的绝对值）：$|1 - (-3)| = 4$，
$S_2 = \frac{1}{2} × 4 × 4 = 8$。
结论： $S_1 = S_2$。
答案：B.

1. 等腰三角形的两个

底角

相等(简写成“等边对

等角

”).

答案：底角;等角.

2. 等腰三角形顶角的平分线平分

底边

,并且垂直于

底边

答案：底边;底边.

3. 如图,在正五边形 $ ABCDE $ 中,连接 $ BE $,则 $ \angle ABE $ 的度数为(

)

A.$ 30^{\circ} $
B.$ 36^{\circ} $
C.$ 54^{\circ} $
D.$ 72^{\circ} $

答案：B.

解析：

解：在正五边形$ABCDE$中，
$\because$正五边形内角和为$(5 - 2)×180^{\circ}=540^{\circ}$，
$\therefore$每个内角$\angle A=\frac{540^{\circ}}{5}=108^{\circ}$。
$\because AB = AE$，
$\therefore\triangle ABE$为等腰三角形，
$\therefore\angle ABE=\angle AEB=\frac{180^{\circ}-\angle A}{2}=\frac{180^{\circ}-108^{\circ}}{2}=36^{\circ}$。
答案：B.

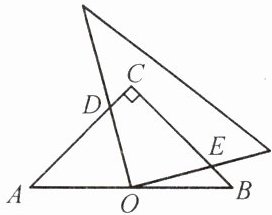
问题如图,在等腰直角 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,点 $ O $ 是 $ AB $ 的中点,且 $ AC = 3 $,将一块直角三角板的直角顶点放在点 $ O $ 处,始终保持该直角三角板的两直角边分别与 $ AC $,$ BC $ 相交,交点分别为 $ D $,$ E $,求 $ CD + CE $ 的值.

名师指导
连接 $ OC $ 构建全等三角形,证明 $ \triangle ODC \cong \triangle OEB $,得 $ DC = BE $,把 $ CD + CE $ 转化到同一条线段上,即求 $ BC $ 的长.
解题示范(学生在教师指导下,独立完成)
证明：

答案：3

解析：

连接OC。
∵△ABC是等腰直角三角形，∠C=90°，AC=3，
∴AC=BC=3，∠A=∠B=45°。
∵O是AB中点，
∴OC=OB，OC平分∠ACB，OC⊥AB，
∴∠OCD=∠BCO=45°=∠B，∠COB=90°。
∵∠DOE=90°，
∴∠DOE=∠COB，
∴∠DOC+∠COE=∠EOB+∠COE，
∴∠DOC=∠EOB。
在△ODC和△OEB中，
∠DOC=∠EOB，
OC=OB，
∠OCD=∠B，
∴△ODC≌△OEB（ASA），
∴DC=BE。
∴CD+CE=BE+CE=BC=3。