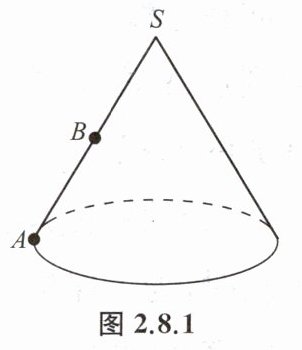
例 2 如图 2.8.1,圆锥的底面半径 $r= 10\ cm$,母线长为 40 cm.
(1)求它的侧面展开图的圆心角和侧面积;
(2)一甲虫从圆锥底面圆上点 A 出发,沿着圆锥侧面绕行到母线 SA 的中点 B,它所走的最短路程是多少厘米?
答案:解:$\text{(1)}$设圆锥侧面展开图的圆心角为n°
依题意得,$\frac{n\pi ×40}{180}=2\pi ×10$
解得$\text{,}n=90$
∴圆锥侧面展开图的圆心角为90°,
侧面积$=\pi ×10×40=400\pi \text{(\,\,cm}^2\text{)}$
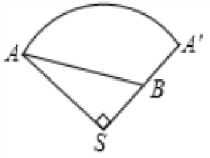
$\left( 2 \right) $如图所示$\text{,}$
由圆锥的侧面展开图可见,从点A爬到点B的最短路程为线段AB的长度.
在Rt△ABS中,∵$AS=A'S=40\,\,\text{cm},$B为A'S的中点
∴$BS=\frac{1}{2}A'S=20\,\,\text{cm}$
∴$AB=\sqrt{40^2+20^2}=20\sqrt{5}\,\,\text{cm}$
∴它所走的最短路程为$20\sqrt{5}\,\,\text{cm}.$
解析:
(1)圆锥底面周长为$2\pi r = 2\pi×10 = 20\pi\ cm$,侧面展开图扇形弧长等于底面周长,设圆心角为$n^\circ$,由$\frac{n\pi×40}{180}=20\pi$,解得$n = 90$,侧面积为$\frac{1}{2}×20\pi×40 = 400\pi\ cm^2$。
(2)将圆锥侧面展开,扇形圆心角$90^\circ$,母线$SA = 40\ cm$,$B$为$SA$中点,所以$SB = 20\ cm$,展开后$A$点对应扇形弧的一个端点,$\angle ASA' = 90^\circ$($A'$为展开后$A$的对应点),则最短路程为$AB$,在$Rt\triangle ASB$中,$AB=\sqrt{SA^2 + SB^2}=\sqrt{40^2 + 20^2}=\sqrt{1600 + 400}=\sqrt{2000}=20\sqrt{5}\ cm$。