6. 如图,半圆的直径AB= 4,C、D是半圆的三等分点,求弦BC、BD与$\overset{\frown}{CD}$围成的图形(阴影部分)的面积.
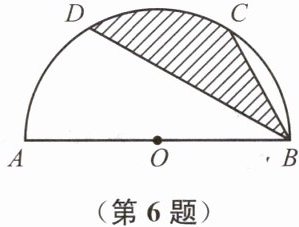
答案: 解:连接OC,OD,CD
∵ C、D是半圆的三等分点
∴ ∠BOC=∠COD=60°∵ OC=OD
∴ △OCD是等边三角形
∴ ∠DCO=∠BOC=60°
∴ CD//AB∴ S△COD=S△CBD
∴$ {S}_{阴影部分}={S}_{扇形COD}={\frac {60π×{(4÷2)}^{2}} {360}}$
$={\frac {2} {3}}π$
解析:
连接OC、OD。
∵AB=4,
∴半径OB=2。
∵C、D是半圆三等分点,
∴∠COD=∠BOC=∠AOD=60°。
∵OC=OD=OB,
∴△OCD、△OBC是等边三角形,∠OBC=60°。
S阴影=S扇形OCD。
S扇形OCD=$\frac{60\pi×2^2}{360}=\frac{2}{3}\pi$。
$\frac{2}{3}\pi$
7. 如图,正方形ABCD的边长为2,分别以点B、C为圆心,以正方形的边长为半径的两圆相交于点P,求图中阴影部分的面积.

答案: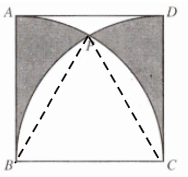
$$解:连接$BP,$$CP,$则$BP=CP=BC=2$
$$则$△BCP$是等边三角形$$
$$
∴$∠BPC=60°,$
∴$∠ABP=90°-60°=30°$
$S_{阴影}=2×[S_{扇形ABP}-(S_{扇形BCP}-S_{BCP})]$
$=2×[\frac {30°}{360°}×π×2²-(\frac {60°}{360°}×π×2²-\frac {1}{2}×2×\sqrt{3})]$
$=2×[\frac {1}{3}π-\frac {2}{3}π+\sqrt{3}]$
$=2\sqrt{3}-\frac {2π}{3}$
解析:
连接BP、CP、AP、DP,BP=CP=BC=2,△BPC为等边三角形,∠PBC=∠PCB=60°,∠ABP=∠DCP=30°。
S扇形ABP=S扇形DCP=$\frac{30°}{360°}×\pi×2^2=\frac{\pi}{3}$,
S△ABP=S△DCP=$\frac{1}{2}×2×2×\sin30°=1$,
阴影部分面积=2×(S扇形ABP-S△ABP)+(S正方形ABCD-S扇形BAPD-S扇形CDPA+S重叠部分),
S扇形BAPD=S扇形CDPA=$\frac{90°}{360°}×\pi×2^2=\pi$,
S重叠部分=2×($\frac{60°}{360°}×\pi×2^2-\frac{\sqrt{3}}{4}×2^2$)=$\frac{2\pi}{3}-2\sqrt{3}$,
S正方形ABCD=4,
阴影部分面积=2×($\frac{\pi}{3}-1$)+(4-π-π+$\frac{2\pi}{3}-2\sqrt{3}$)=2×$\frac{\pi}{3}-2+4-2\pi+\frac{2\pi}{3}-2\sqrt{3}=2\sqrt{3}-\frac{2\pi}{3}$。
$2\sqrt{3}-\frac{2\pi}{3}$
8.(1)如图①,将含30°角的三角尺ABC的斜边放置在直线l上,并按顺时针方向在直线l上翻动两次,使它翻到△A″B″C″的位置上,设斜边AB= 2,则点A运动到点A″的位置时,点A经过的路线长
$\frac {4}{3}π$
,点A经过的路线与直线l所围成的面积为
$\frac {25}{12}π+\frac {\sqrt {3}}{2}$
.
(2)如图②,已知半圆形工件的半圆直径为4m,将它的直径平行于地面放置,搬动时,为了保护圆弧部分不受损伤,先将半圆形工件做如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移50m.求圆心O所经过的路线长
(50+2π)m
.
答案:$(\frac 43+\frac {\sqrt {3}}2)π$
$ \frac {25}{12}π+\frac {\sqrt {3}}2$
(50+2π)m.