例1 (1)已知扇形的弧长为6π,半径为4,则扇形的圆心角度数为
270°
,面积为
12π
.
(2)已知扇形的圆心角为60°,面积为6π,则扇形的半径为
6
.
(3)如果一个半径为2的圆的面积恰好与一个半径为4的扇形面积相等,那么这个扇形的圆心角度数为
90°
.
(4)如图2.7.1,分别以等边三角形ABC的三个顶点为圆心,边长为半径画弧,得到的封闭图形是“莱洛三角形”.若AB= 2,则此莱洛三角形的周长为
2π
,面积为
2π-2√3
.
答案:(1)270°,12π;(2)6;(3)90°;(4)2π,2π-2√3
解析:
(1)设扇形圆心角为$n^{\circ}$,由弧长公式$l = \frac{n\pi r}{180}$,得$6\pi=\frac{n\pi×4}{180}$,解得$n = 270$;面积$S=\frac{1}{2}lr=\frac{1}{2}×6\pi×4 = 12\pi$,故答案为$270^{\circ}$,$12\pi$。
(2)设扇形半径为$r$,由面积公式$S=\frac{n\pi r^{2}}{360}$,得$6\pi=\frac{60\pi r^{2}}{360}$,解得$r = 6$,故答案为$6$。
(3)设扇形圆心角为$n^{\circ}$,圆面积$\pi×2^{2}=4\pi$,扇形面积$\frac{n\pi×4^{2}}{360}=4\pi$,解得$n = 90$,故答案为$90^{\circ}$。
(4)等边三角形内角$60^{\circ}$,每个弧长$\frac{60\pi×2}{180}=\frac{2\pi}{3}$,周长$3×\frac{2\pi}{3}=2\pi$;每个弓形面积$\frac{60\pi×2^{2}}{360}-\frac{\sqrt{3}}{4}×2^{2}=\frac{2\pi}{3}-\sqrt{3}$,总面积$3×(\frac{2\pi}{3}-\sqrt{3})=2\pi - 3\sqrt{3}$,故答案为$2\pi$,$2\pi - 2\sqrt{3}$。
例2 如图2.7.2,⊙O的半径为R,直径AB⊥CD,以点B为圆心,以BC为半径画$\overset{\frown}{CED}$.求$\overset{\frown}{CED}与\overset{\frown}{CAD}$围成的阴影区域的面积S.
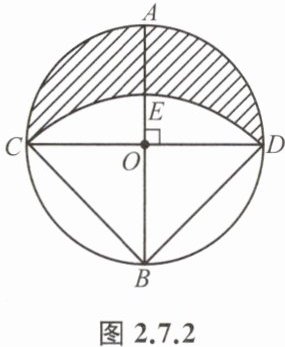
答案:$$解:
∵$CD$是$⊙O$的直径,$$
$$
∴$∠CBD=90°,$$$
$$
∴$S_{△CBD}=\frac {1}{2}×CD×OB=\frac {1}{2}×2R×R=R^2,$$$
$$
∵$⊙O$的半径为$R,$$AB⊥CD,$$$
$$
∴$BC=BD=\sqrt{2}R,$$$
$$
∵$CD$是$⊙O$的直径,$$
$$
∴$∠CBD=90°,$$$
$$
∴$S_{扇形CBD}=\frac {1}{2}×\frac {π}{2}×BC^2$
$=\frac {π}{2}R^2,$$$
$$
∴$S_{阴影ACED}= S_{半圆ACD}-S_{弓形}= S_{半圆ACD}-(S_{扇形CBD}-S_{△CBD})$
$=\frac {1}{2}πR^2-(\frac {π}{2}R^2-R^2)$
$=R^2.$
解析:
连接BC,BD。
∵AB,CD为⊙O直径且AB⊥CD,⊙O半径为R,
∴OC=OD=OB=R,∠COB=∠DOB=90°,
∴BC=BD=$\sqrt{OC^2+OB^2}=\sqrt{R^2+R^2}=\sqrt{2}R$。
S阴影=S半圆CAD-(S扇形BCE+S扇形BDE-S△CBD)
∵S半圆CAD=$\frac{1}{2}\pi R^2$,
S扇形BCE=S扇形BDE=$\frac{90\pi (\sqrt{2}R)^2}{360}=\frac{1}{2}\pi R^2$,
S△CBD=$\frac{1}{2}CD\cdot OB=\frac{1}{2}×2R× R=R^2$,
∴S阴影=$\frac{1}{2}\pi R^2$-($\frac{1}{2}\pi R^2+\frac{1}{2}\pi R^2-R^2$)=R2。
答:阴影区域的面积S为R2。