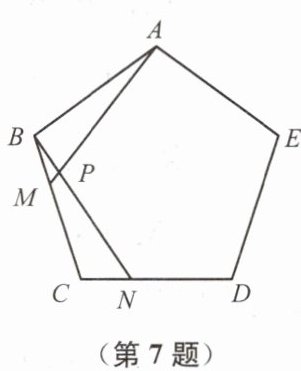
7. 如图,在正五边形$ABCDE$中,点$M、N分别在边BC、CD$上,且$BM= CN$,$AM与BN相交于点P$.
(1)求证:$\triangle ABM\cong\triangle BCN$;
(2)求$\angle APN$的度数.
答案:证明:(1)因为五边形ABCDE是正五边形,
所以AB=BC,$\angle ABM= \angle BCN.$
因为在$\triangle ABM$与$\triangle BCN$中,
AB=BC,$\angle ABM=\angle \mathit{B}\mathit{C}\mathit{N},$$BM=\mathit{C}\mathit{N},$
所以$\triangle ABM≌\triangle BCN.$
(2)因为$\triangle ABM≌\triangle BCN,$
所以$\angle MBP= \angle BAP.$
因为$\angle MBP+ \angle BMP+ \angle BPM= \angle BAP+ \angle BMA+ \angle MBA=180^{ \circ },$
所以$\angle BPM= \angle MBA,$
所以$\angle APN= \angle MBA,$
所以$\angle MBA=\angle APN=\dfrac{(5-2)\times 180}{5}={108}^{\circ }.$
解析:
(1)证明:因为ABCDE是正五边形,所以AB=BC,∠ABM=∠BCN。又因为BM=CN,所以△ABM≌△BCN(SAS)。
(2)由(1)知△ABM≌△BCN,所以∠BAM=∠CBN。因为∠APN=∠BAM+∠ABN,所以∠APN=∠CBN+∠ABN=∠ABC。正五边形内角和为(5-2)×180°=540°,每个内角∠ABC=540°÷5=108°,故∠APN=108°。
8. 如图,在正八边形$ABCDEFGH$中,四边形$BCFG的面积为20\ cm^2$,则正八边形的面积为______$cm^2$.

40
答案:40
解析:
设正八边形边长为$a$,将正八边形补成一个正方形,四个角为等腰直角三角形,直角边长为$\frac{a}{\sqrt{2}}$。
正方形边长为$a + 2×\frac{a}{\sqrt{2}} = a(1+\sqrt{2})$,面积为$a^2(1+\sqrt{2})^2 = a^2(3 + 2\sqrt{2})$。
四个等腰直角三角形面积和为$4×\frac{1}{2}×(\frac{a}{\sqrt{2}})^2 = a^2$,正八边形面积为$a^2(3 + 2\sqrt{2}) - a^2 = a^2(2 + 2\sqrt{2})$。
四边形$BCFG$为矩形,长为$a(1+\sqrt{2})$,宽为$a$,面积$a^2(1+\sqrt{2}) = 20$。
正八边形面积为$2× a^2(1+\sqrt{2}) = 40$。
40
9. 某厂家要设计一个装彩色铅笔的纸盒,已知每支笔形状、大小相同,底面均为边长为$1\ cm$的正六边形.目前厂家提供了圆形和等边三角形两种纸盒底面设计方案,我们以6支彩色铅笔为例,可以设计如图的两种收纳方案.这两种方案中底面积分别是
9πcm²
、
$12\sqrt{3}cm²$
.
答案:9πcm²
$12\sqrt{3}cm²$