6. 如图,⊙O分别切△ABC的边AB、BC、CA于点D、E、F,∠B= 70°,∠C= 60°,M是$\overset{\frown}{DEF}$上的动点(与点D、F不重合).∠DMF的大小确定吗?若确定,求∠DMF的度数;若不确定,请说明理由.
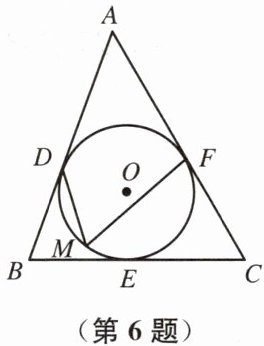
答案:解:∠DMF的大小确定,连接OD,OF,如图所示
∵ AB,BC,CA为⊙O的切线
∴ OD⊥AB,OF⊥AC∴ ∠ODA=∠OFA=90°
∵ ∠B=70°,∠C=60°
∴ ∠A=180°-70°-60°=50°
∴ ∠DOF=360°-90°-90°-50°=130°
∴$ ∠DMF=\frac 12 ∠DOF=65°$
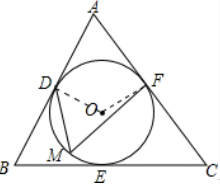
解析:
连接OD,OF。
在△ABC中,∠A=180°-∠B-∠C=180°-70°-60°=50°。
∵⊙O分别切AB、AC于点D、F,
∴OD⊥AB,OF⊥AC,
∴∠ODA=∠OFA=90°。
在四边形ADOF中,∠DOF=360°-∠ODA-∠OFA-∠A=360°-90°-90°-50°=130°。
∵M是$\overset{\frown}{DEF}$上的动点(与点D、F不重合),
∴∠DMF=$\frac{1}{2}$∠DOF=$\frac{1}{2}$×130°=65°。
∠DMF的大小确定,为65°。
7. 已知:如图,⊙O为△ABC的内切圆,⊙O'为△ABC的外接圆.
求证:AD= CD= OD.

答案:证明:∵圆O为△ABC的内切圆
∴O是△ABC角平分线的交点
∴∠ABO=∠CBO,∠BAO=∠CAO
根据在同圆或等圆中,相等的圆周角所对的弧相等,
所对的弦相等,可得,弧AD=弧 CD
∴AD= CD∵CD所对的圆周角是∠CAD和∠CBD
∴∠CAD=∠CBO∴∠CAD=∠ABO
∴∠CAO+∠CAD=∠BAO+∠ABO
∴∠OAD=∠BAO+∠ABO
又∵∠AOD=∠BAO+∠ABO
∴∠OAD=∠AOD∴AD= OD∴AD= CD= OD
8. 如图,在△ABC中,∠C= 90°,AC= 6,AB= 10,D是BC边的中点,以AD上一点O为圆心的圆与AB、BC都相切,则⊙O的半径为(
A
)
A.$\frac{12}{7}$
B.$\frac{1}{5}$
C.$\frac{5}{3}$
D.2
答案:A
解析:
在△ABC中,∠C=90°,AC=6,AB=10,由勾股定理得BC=√(AB²-AC²)=√(10²-6²)=8。
D是BC中点,CD=BC/2=4,AD=√(AC²+CD²)=√(6²+4²)=2√13。
设⊙O半径为r,圆心O到AB、BC距离均为r。过O作OE⊥AB于E,OF⊥BC于F,则OE=OF=r,四边形OEBF为矩形,OF=BE=r,AE=AB-BE=10-r。
sin∠BAD=OE/AO=r/AO,cos∠BAD=AE/AO=(10-r)/AO。
在Rt△ACD中,sin∠CAD=CD/AD=4/(2√13)=2√13/13,cos∠CAD=AC/AD=6/(2√13)=3√13/13。
∠BAD=∠BAC-∠CAD,sin∠BAD=sin(∠BAC-∠CAD)=sin∠BACcos∠CAD - cos∠BACsin∠CAD。
sin∠BAC=BC/AB=8/10=4/5,cos∠BAC=AC/AB=6/10=3/5,
sin∠BAD=4/5×3√13/13 - 3/5×2√13/13=12√13/65 - 6√13/65=6√13/65,
即r/AO=6√13/65,AO=65r/(6√13)=5√13r/6。
cos∠BAD=cos(∠BAC-∠CAD)=cos∠BACcos∠CAD + sin∠BACsin∠CAD=3/5×3√13/13 + 4/5×2√13/13=9√13/65 + 8√13/65=17√13/65,
即(10-r)/AO=17√13/65,将AO=5√13r/6代入得(10-r)/(5√13r/6)=17√13/65,
(6(10-r))/(5√13r)=17√13/65,6(10-r)×65=17√13×5√13r,390(10-r)=1105r,3900 - 390r=1105r,1495r=3900,r=12/7。
答案:$\frac{12}{7}$
9. 如图,将三角形纸片ABC沿直线DE折叠,点A恰好与△ABC的内心I重合,若∠DIB+∠EIC= 195°,则∠BAC的度数是(
B
)
A.40°
B.50°
C.60°
D.70°
答案:B