2025年课课练九年级数学上册苏科版第65页解析答案

例2 为美化校园,学校准备在如图2.5.5所示的三角形空地上修建一个圆形花坛,且要使花坛的面积最大.
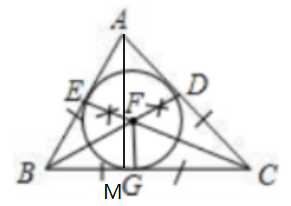
(1)请在图中画出这个圆形花坛(用直尺和圆规作图,不写作法,但要保留作图痕迹).
(2)若AB= 4m,AC= 5m,BC= 6m,求(1)中所画圆形花坛的半径.

答案：
解：(1)如图所示
$\text{(2)作}AM⊥BC\text{，垂足为点}M.$
设$BM=x\,\,\text{m}，$则$CM=\text{(}6-x\text{)\ m}$
在Rt△ABM中，由勾股定理可知，
$AM^2＋BM^2=AB^2$∵$AB=4\ \text{m}，$$BM=x\ \text{m}$
∴$AM^2=AB^2-BM^2=16-x^2$
在Rt△ACM中，由勾股定理可知，
$AM^2+CM^2=AC^2$
∵$CM=\left( 6-x \right) \ \text{m,\ }AC=5\ \text{m}$
∴$16-x^2+\left( 6-x \right) ^2=5^2$解得$x=\frac{9}{4}$
∴$BM=\frac{9}{4}\ \text{m,\ }AM=\frac{5\sqrt{7}}{4}\ \text{m}$
∴$S_{△ABC}=\frac{1}{2}×6×\frac{5\sqrt{7}}{4}=\frac{15\sqrt{7}}{4}\ \text\ \mathrm {{m}^2}$
设所画圆形花坛的半径为$\ r\ \text{m}，$
则$\frac{1}{2}×\text{(}4+5+6\text{)}r=\frac{15\sqrt{7}}{4}$解得，$r=\frac{\sqrt{7}}{2}$
∴所画圆形花坛的半径为$\frac{\sqrt{7}}{2}\ \text{m}.$

1. 下列命题中,正确的是(

)
A.三角形的内心到三角形三个顶点的距离相等
B.三角形的内心不一定在三角形的内部
C.等边三角形的内心与外心重合
D.一个圆一定有唯一一个外切三角形

答案：C

2. 在Rt△ABC中,∠C= 90°,AC= 3,AB= 5,它的内切圆与外接圆的半径分别为(

)
A.1,2.5
B.2,5
C.1.5,2.5
D.2,2.5

答案：A

解析：

在Rt△ABC中，∠C=90°，AC=3，AB=5。
由勾股定理得：BC=$\sqrt{AB^2 - AC^2}=\sqrt{5^2 - 3^2}=4$。
外接圆半径：$R=\frac{AB}{2}=\frac{5}{2}=2.5$。
内切圆半径：$r=\frac{AC + BC - AB}{2}=\frac{3 + 4 - 5}{2}=1$。
A.

3. 若等边三角形的边长为2,则它的内切圆面积为

$\frac{1}{3}π$

答案：$\frac{1}{3}π$

解析：

设等边三角形的内切圆半径为$r$。
等边三角形的边长为$2$，其高$h = \sqrt{2^2 - 1^2} = \sqrt{3}$。
根据等边三角形面积公式，面积$S = \frac{1}{2} × 2 × \sqrt{3} = \sqrt{3}$。
又因为等边三角形面积也可表示为$S = \frac{1}{2} × (2 + 2 + 2) × r = 3r$，所以$3r = \sqrt{3}$，解得$r = \frac{\sqrt{3}}{3}$。
内切圆面积$S = \pi r^2 = \pi × (\frac{\sqrt{3}}{3})^2 = \frac{1}{3}\pi$。
$\frac{1}{3}\pi$

4. 已知△ABC的面积为$8cm^2,$周长为24cm,则△ABC内切圆的半径为

$\frac{2}{3}$

cm.

答案：$\frac{2}{3}$

解析：

设△ABC内切圆的半径为$r$cm，周长为$C$，面积为$S$。
因为三角形面积$S = \frac{1}{2}Cr$，已知$S = 8$，$C = 24$，所以$8=\frac{1}{2}×24× r$，解得$r=\frac{2}{3}$。
$\frac{2}{3}$

5. 已知△ABC的内心为O,∠BOC= 110°,则∠BAC= ______°.

答案：40

解析：

∵O是△ABC的内心，
∴OB平分∠ABC，OC平分∠ACB，
∴∠OBC=$\frac{1}{2}$∠ABC，∠OCB=$\frac{1}{2}$∠ACB，
在△BOC中，∠BOC=110°，
∴∠OBC+∠OCB=180°-∠BOC=180°-110°=70°，
∴$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=70°，
∴∠ABC+∠ACB=140°，
在△ABC中，∠BAC=180°-(∠ABC+∠ACB)=180°-140°=40°．
40