例2 如图2.2.4,AB、CD是⊙O的弦,且AB//CD.$\overset{\frown}{AC}与\overset{\frown}{BD}$相等吗?为什么?
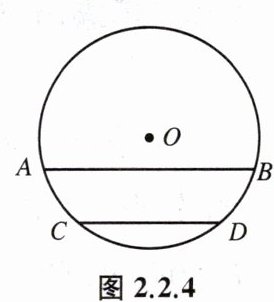
答案:解:$\overset{\LARGE{ \frown}}{ AC}=\overset{\LARGE{ \frown}}{ BD}$
理由:连接AD,BC
∵AB//CD,
∴∠ABC=∠BCD
∴∠ABC=∠ADC,
∴∠BCD=∠ADC
∴$\overset{\LARGE{ \frown}}{ AC}=\overset{\LARGE{ \frown}}{ BD}$
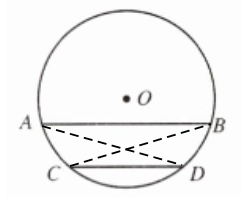
解析:
$\widehat{AC}=\widehat{BD}$.
连接$AD$.
因为$AB// CD$,所以$\angle BAD=\angle ADC$.
所以$\widehat{AC}=\widehat{BD}$.
1. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,AB= 20,CD= 16,则线段OE的长为(
B
)
A.4
B.6
C.8
D.10
答案:B
解析:
连接OC,
∵AB是⊙O的直径,AB=20,
∴OC=OA=10,
∵CD⊥AB,CD=16,
∴CE=DE=8,∠OEC=90°,
在Rt△OEC中,OE²+CE²=OC²,
OE²+8²=10²,
OE²=36,
OE=6,
B
2. 如图,CD是⊙O的直径,弦AB⊥CD,垂足为E,CE= 1,AB= 10,则直径CD的长为(
D
)
A.12.5
B.13
C.25
D.26
答案:D
解析:
连接OA,设⊙O的半径为$r$,则$OA = OC = r$。
因为$CE = 1$,所以$OE = OC - CE = r - 1$。
由于$AB \perp CD$,$AB = 10$,根据垂径定理,$AE = \frac{1}{2}AB = 5$。
在$Rt\triangle AOE$中,由勾股定理得:$OA^2 = AE^2 + OE^2$,即$r^2 = 5^2 + (r - 1)^2$。
解得$r = 13$,故直径$CD = 2r = 26$。
D
3. 如图,已知⊙O的半径为5,弦AB= 6,M是AB上的任意一点,则线段OM的长可能是(
C
)

A.2.5
B.3.5
C.4.5
D.5.5
答案:C
解析:
过点O作OH⊥AB于点H,连接OA。
∵AB=6,OH⊥AB,
∴AH=HB=3。
∵OA=5,
∴在Rt△OAH中,OH=$\sqrt{OA^2 - AH^2}=\sqrt{5^2 - 3^2}=4$。
∵M是AB上任意一点,
∴OH≤OM≤OA,即4≤OM≤5。
选项中符合条件的是4.5。
C
4. 如图,AB是半圆O的直径,OD⊥AC,垂足为D,OD= 2,则弦BC的长为
4
.
答案:4
解析:
∵AB是半圆O的直径,
∴O是AB的中点。
∵OD⊥AC,
∴AD=DC,即D是AC的中点。
∴OD是△ABC的中位线。
∴BC=2OD。
∵OD=2,
∴BC=2×2=4。
4
5. 如图,将半径为2 cm的圆形纸片折叠后,圆弧恰好经过圆心O,折痕AB的长为
$2\sqrt{3}\ \mathrm {cm}$
.
答案:$2\sqrt{3}\ \mathrm {cm}$
解析:
连接OA,过点O作OC⊥AB于点C,则AC=BC。
由折叠性质知,点O到AB的距离OC=$\frac{1}{2}$OA=1cm。
在Rt△OAC中,OA=2cm,OC=1cm,
$AC=\sqrt{OA^{2}-OC^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$cm,
AB=2AC=2$\sqrt{3}$cm。
$2\sqrt{3}$ cm