10. 如图,MN 是$\odot O$的直径,$MN= 2cm$,A 是半圆上的三等分点,B 是$\widehat {AN}$的中点,P 是直径 MN 上的动点,则$PA+PB$的最小值为(
B
)
A.$2\sqrt {2}cm$
B.$\sqrt {2}cm$
C.1 cm
D.2 cm
答案:B
解析:
作点A关于MN的对称点A',连接A'B交MN于点P,此时PA+PB最小,最小值为A'B的长。
连接OA,OA',OB。
∵MN是直径,MN=2cm,
∴OA=OA'=OB=1cm。
∵A是半圆上的三等分点,
∴∠AON=60°。
∵B是$\widehat{AN}$的中点,
∴∠BON=30°。
∵点A与A'关于MN对称,
∴∠A'ON=∠AON=60°。
∴∠A'OB=∠A'ON+∠BON=60°+30°=90°。
在Rt△A'OB中,A'B=$\sqrt{OA'^2+OB^2}=\sqrt{1^2+1^2}=\sqrt{2}$cm。
即PA+PB的最小值为$\sqrt{2}$cm。
B.
11. 如图,AB 是$\odot O$的直径,弦 CD 交 AB 于点 M,且$OM= CM$.求证:$\widehat {AD}= 3\widehat {BC}.$
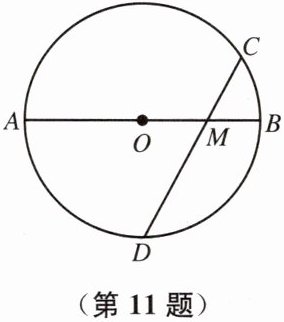
答案:证明:连接OC,OD.
设∠BOC=α,则弧BC的度数为α.
∵OM=CM,∴△OMC为等腰三角形,∠MCO=∠MOC=α.
∵OC=OD,∴△ODC为等腰三角形,∠ODC=∠OCD=α.
在△CDM中,∠CMD=180°-∠MCD-∠MDC=180°-α-α=180°-2α.
∵∠CMD+∠OMD=180°,∴∠OMD=180°-(180°-2α)=2α.
在△ODM中,∠DOM=180°-∠ODM-∠OMD=180°-α-2α=180°-3α.
∵AB为直径,∠AOD+∠DOM=180°,∴∠AOD=180°-∠DOM=180°-(180°-3α)=3α.
∵∠AOD为弧AD所对圆心角,∠BOC为弧BC所对圆心角,
∴弧AD的度数=∠AOD=3α,弧BC的度数=∠BOC=α,
∴弧AD=3弧BC.
例1 如图2.2.3,⊙O的直径AB= 12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP∶AP= 1∶5.求CD的长.

答案:解:连接OC
∵AB=12,BP∶AP=1∶5
∴$BP=\frac 16AB=2,$$AP=\frac 56AB=10,$OA=6
∴OP=AP-OA=4
∵OC=OA=6,OP=4
∴在Rt△OCP 中,$CP=\sqrt {OC^2-OP^2}=\sqrt {6^2-4^2}=2\sqrt {5}$
∵CD⊥AB
∴$CD=2CP=4\sqrt {5}$
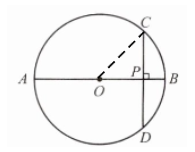
解析:
连接OC,
∵AB=12,BP∶AP=1∶5,
∴AP=10,BP=2,
∵OA=OB=OC=6,
∴OP=OB-BP=6-2=4,
∵CD⊥AB,
∴CP=DP,∠OPC=90°,
在Rt△OPC中,CP=$\sqrt{OC^2-OP^2}=\sqrt{6^2-4^2}=2\sqrt{5}$,
∴CD=2CP=4\sqrt{5}。