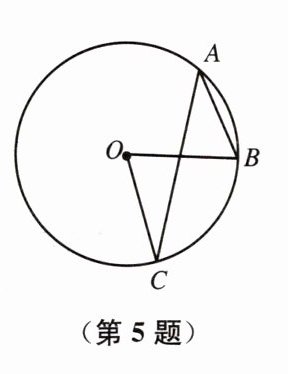
5. 如图,点A、B、C在⊙O上,∠A= 36°,∠C= 28°,则∠B= ______.
64°
答案:64°.
解析:
连接OB。
∵OA=OB=OC,
∴∠OAB=∠OBA=36°,∠OCB=∠OBC=28°。
∠B=∠OBA+∠OBC=36°+28°=64°。
64°
6. 把一张半圆形纸片按如图所示的方式折叠后展开,折痕为AB,则$\overset{\frown}{AB}$所对圆心角的度数是
120°
.
答案:120°.
解析:
设半圆的圆心为$O$,半圆的直径为$CD$,折叠后半圆的圆弧与直径$CD$相切于点$O$。连接$OA$、$OB$,则$OA=OB$为半圆的半径。由折叠性质知,$AB$垂直平分折叠后圆弧的圆心与点$O$的连线,设折叠后圆弧的圆心为$O'$,则$OO'\perp AB$,且$OO'=\frac{1}{2}OA$。在$Rt\triangle OO'A$中,$\cos\angle AOO'=\frac{OO'}{OA}=\frac{1}{2}$,所以$\angle AOO' = 60^\circ$,同理$\angle BOO' = 60^\circ$,故$\angle AOB=\angle AOO'+\angle BOO' = 120^\circ$,即$\overset{\frown}{AB}$所对圆心角的度数是$120^\circ$。
$120^\circ$
7. 如图,AB、CD为⊙O的两条直径,点E、F在直径CD上,且CE= DF.
求证:AF= BE.

答案:证明:∵CE=DF,CO=DO
∴EO=FO
在△OBE和△OAF中,
∴$△OBE≌△OAF\left( SAS \right) $
∴AF=BE
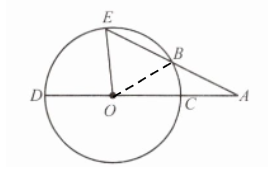
8. 如图,CD是⊙O的直径,∠EOD= 84°,AE交⊙O于点B,且AB= OC.求∠A的度数.

答案:解:连接OB
∵AB=OC
∴AB= BO
∴∠BOC=∠A
∴∠EBO=∠BOC+∠A= 2∠A
∵OB= OE
∴∠E=∠EBO=2∠A
∴∠EOD=∠E+∠A=3∠A
∵∠EOD=84°
∴3∠A=84°
∴∠A=28°
解析:
连接OB,设∠A=x。
因为AB=OC,OB=OC(同圆半径相等),所以AB=OB,故∠AOB=∠A=x。
∠OBE是△AOB的外角,所以∠OBE=∠A+∠AOB=2x。
因为OB=OE(同圆半径相等),所以∠E=∠OBE=2x。
在△AOE中,∠EOD是外角,∠EOD=∠A+∠E,即84°=x+2x,解得x=28°。
∠A=28°