答案：1. （1）
首先求$A$、$B$两点坐标：
对于一次函数$y = \frac{3}{4}x + 3$，当$x = 0$时，$y=3$，所以$B(0,3)$；当$y = 0$时，$0=\frac{3}{4}x + 3$，解得$x=-4$，所以$A(-4,0)$。
根据两点间距离公式$d=\sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$，可得$\vert AB\vert=\sqrt{(-4 - 0)^2+(0 - 3)^2}=\sqrt{16 + 9}=5$。
然后求$O$到$AB$的距离$h$：
根据三角形面积公式$S_{\triangle AOB}=\frac{1}{2}\vert OA\vert×\vert OB\vert=\frac{1}{2}\vert AB\vert× h$，已知$\vert OA\vert = 4$，$\vert OB\vert = 3$，$\vert AB\vert = 5$，则$\frac{1}{2}×4×3=\frac{1}{2}×5× h$，解得$h=\frac{12}{5}$。
最后求$\triangle ABP$面积的最大值：
因为$P$是$\odot O$上的动点，$\odot O$半径$r = 2$，$P$到$AB$的最大距离$H=h + r$（当$OP\perp AB$时）。
$H=\frac{12}{5}+2=\frac{12 + 10}{5}=\frac{22}{5}$。
根据三角形面积公式$S_{\triangle ABP}=\frac{1}{2}\vert AB\vert× H$，把$\vert AB\vert = 5$，$H=\frac{22}{5}$代入，得$S_{\triangle ABP}=\frac{1}{2}×5×\frac{22}{5}=11$。
2. （2）
连接$AM$：
因为点$B$关于直线$AP$的对称点是$M$，所以$AM = AB = 3$。
所以点$M$在以$A$为圆心，$AB$长为半径的圆上。
然后求$MC$的最小值：
根据三角形三边关系$\vert MC\vert\geqslant\vert AC\vert-\vert AM\vert$。
在矩形$ABCD$中，$AB = 3$，$BC = 4$，根据勾股定理$\vert AC\vert=\sqrt{AB^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}} = 5$，$AM = AB = 3$。
所以$MC$的最小值为$\vert AC\vert-\vert AM\vert=5 - 3=2$。
故答案为：（1）$11$；（2）$2$。

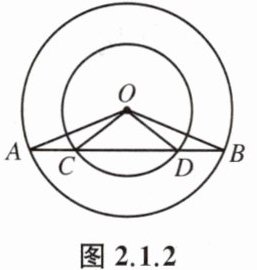
答案：​解：相等，理由如下：​
​∵OC=OD，OA=OB​
​∴∠OCD=∠ODC，∠OAB=∠OBA​
​∴∠OCD-∠OAB=∠ODC-∠OBA，​
​即∠AOC=∠BOD​