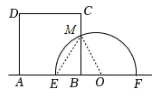
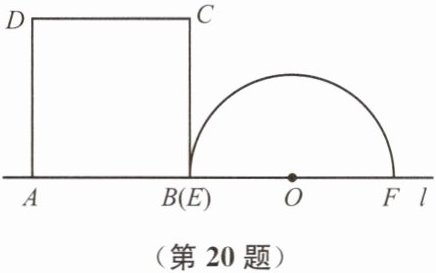
20. (本题8分)如图,矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E、F都在直线l上,且AB= 7,EF= 10,BC>5.点B以1个单位长度每秒的速度从点E处出发,沿射线EF方向运动,矩形ABCD随之运动,运动时间为ts.
(1) 求当t= 2.5时半圆O在矩形ABCD内的弧的长度.
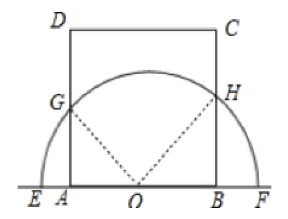
(2) 在点B运动的过程中,当AD、BC都与半圆O相交时,设这两个交点为G、H.连接OG、OH.若∠GOH为直角,求此时t的值.
答案:解:(1)设BC与⊙O交于点M,当t=2.5时,BE=2.5,
∵EF=10,∴$OE=\frac {1}{2}EF=5,$
∴OB=2.5,∴EB=OB,
在矩形ABCD中,∠ABC=90°,∴ME=MO,
又∵MO=EO,∴ME=EO=MO,
∴△MOE是等边三角形,∴∠EOM=60°,
∴$l_{ME}=\frac {60π×5}{180}=\frac {5π}{3}.$
∴半圆O在矩形ABCD内的弧的长度为$\frac {5π}{3}.$
(2)连接GO,HO,∵∠GOH=90°,∴∠AOG+∠BOH=90°,
∵∠AGO+∠AOG=90°,∴∠AGO=∠BOH,
在△AGO和△OBH中,
$\begin{cases}∠AGO=∠BOH\\∠GAO=∠HBO\\OG=OH\end{cases}$
∴$△AGO≌△BOH(\mathrm {AAS}),$
∴OB=AG=t-5,∵AB=7,∴AE=t-7,
∴AO=5-(t-7)=12-t,在Rt△AGO中,$AG^2+AO^2=OG^2,$
∴$(t-5)^2+(12-t)^2=5^2,$
解得:$t_1=8,$$t_2=9,$即t的值为8或9.