17. (本题6分)小明去某体育馆锻炼,该体育馆有A、B两个进馆通道和C、D、E三个出馆通道,从每个进馆通道进馆的可能性相同,从每个出馆通道出馆的可能性也相同.
(1) 用列表或画树状图的方法列出小明一次进出体育馆经过通道的所有等可能的结果;
(2) 求小明恰好经过通道A与通道D的概率.
答案:1. (1)画树状图:
首先,进馆通道有$A$、$B$两种情况,出馆通道有$C$、$D$、$E$三种情况。
树状图如下:
第一层:从起点开始,第一个分支为进馆通道$A$,第二个分支为进馆通道$B$。
第二层:若进馆通道为$A$,则出馆通道有$C$、$D$、$E$三个分支;若进馆通道为$B$,则出馆通道也有$C$、$D$、$E$三个分支。
所以所有等可能的结果为$(A,C)$,$(A,D)$,$(A,E)$,$(B,C)$,$(B,D)$,$(B,E)$。
2. (2)
解:
由(1)可知,所有等可能的结果共有$n = 6$种。
小明恰好经过通道$A$与通道$D$的结果只有$m = 1$种。
根据概率公式$P=\frac{m}{n}$,这里$n$是所有等可能结果的总数,$m$是事件发生的结果数。
所以$P=\frac{1}{6}$。
综上,(1)所有等可能结果为$(A,C)$,$(A,D)$,$(A,E)$,$(B,C)$,$(B,D)$,$(B,E)$;(2)小明恰好经过通道$A$与通道$D$的概率为$\frac{1}{6}$。
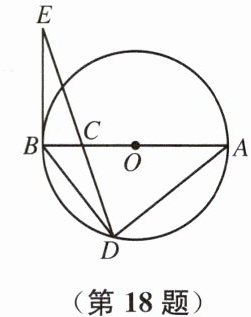
18. (本题8分)如图,AB为⊙O的直径,点C在直径AB上,OC= 3,点D在⊙O上且满足AC= AD,连接DC并延长到E点,使BE= BD.
(1) 求证:BE是⊙O的切线.
(2) 当BE= 6时,求⊙O半径的长.
答案:1. (1)证明:
因为$AC = AD$,所以$\angle ADC=\angle ACD$。
又因为$\angle ACD=\angle BCE$,所以$\angle ADC=\angle BCE$。
因为$OB = OD$,所以$\angle OBD=\angle ODB$。
因为$BE = BD$,所以$\angle BDE=\angle E$。
因为$AB$是$\odot O$的直径,所以$\angle ADB = 90^{\circ}$,即$\angle ODB+\angle ADC = 90^{\circ}$。
则$\angle OBD+\angle BCE+\angle E=90^{\circ}$,即$\angle OBD+\angle BDE+\angle E = 90^{\circ}$,也就是$\angle OBE = 90^{\circ}$。
因为$OB$是$\odot O$的半径,$OB\perp BE$,所以$BE$是$\odot O$的切线。
2. (2)解:
设$\odot O$的半径为$r$,则$OA = OB = r$,$AC=AD$,$OC = 3$,所以$AC=AD=r + 3$。
因为$BE = BD = 6$,$\angle ADB=\angle OBE = 90^{\circ}$。
在$Rt\triangle ABD$中,根据勾股定理$AB^{2}=AD^{2}+BD^{2}$,$AB = 2r$,$AD=r + 3$,$BD = 6$。
所以$(2r)^{2}=(r + 3)^{2}+6^{2}$。
展开得$4r^{2}=r^{2}+6r + 9+36$。
移项得$4r^{2}-r^{2}-6r-9 - 36 = 0$。
合并同类项得$3r^{2}-6r-45 = 0$,两边同时除以$3$得$r^{2}-2r - 15 = 0$。
因式分解得$(r - 5)(r+3)=0$。
解得$r_{1}=5$,$r_{2}=-3$(半径不能为负舍去)。
所以$\odot O$半径的长为$5$。