13. 在甲、乙两个不透明的口袋中,分别装有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字1、2、3、4,乙口袋中的小球上分别标有数字2、3、4.先从甲口袋中任意摸出一个小球,记下数字为m,再从乙口袋中任意摸出一个小球,记下数字为n.
(1)请用列表或画树状图的方法表示出(m,n)所有可能的结果.
(2)若m、n都是方程$x^{2}-5x+6= 0$的解,则小敏获胜;若m、n都不是方程$x^{2}-5x+6= 0$的解,则小明获胜.他们两人谁获胜的概率大?
答案:解:(1)如图:
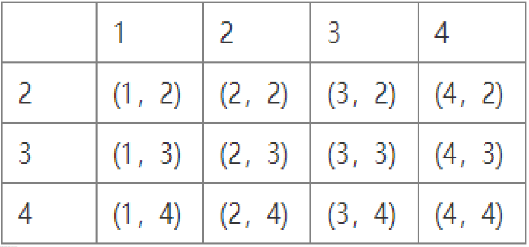
$(2){x}^2-5x+6=0$
(x-2)(x-3)=0
x-2=0或x-3=0
${x}_1=2,$${x}_2=3$
∵当(m,n)为(2,2),(2,3),(3,2)或(3,3)时,小敏获胜
∴P(小敏获胜$)=\frac 4 {12}=\frac 1 3$
∵当(m,n)为(1,4),或(4,4)时,小明获胜
P(小明获胜$)=\frac {2}{12}=\frac 16$
∴小敏获胜的概率大.