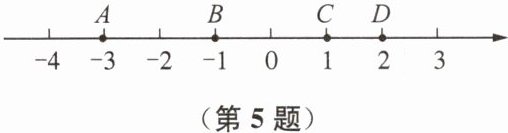
5. 如图,数轴上的点A、B、C、D表示的数分别为-3、-1、1、2,从A、B、C、D四点中任意取两点,求所取两点之间的距离恰好为2的概率.
答案:解:共有6种等可能的结果,
所取两点距离恰好为2的结果占其中的2种。
∴P(所取两点距离恰好为$2)=\frac 26=\frac 13$
解析:
从A、B、C、D四点中任意取两点,所有可能的组合为:AB、AC、AD、BC、BD、CD,共6种。
计算各组合两点之间的距离:
AB:$|-1 - (-3)| = 2$
AC:$|1 - (-3)| = 4$
AD:$|2 - (-3)| = 5$
BC:$|1 - (-1)| = 2$
BD:$|2 - (-1)| = 3$
CD:$|2 - 1| = 1$
距离恰好为2的组合有AB、BC,共2种。
概率为$\frac{2}{6} = \frac{1}{3}$。
$\frac{1}{3}$
6. 某超市在开业周年时举行摸球抽奖活动.规则如下:在一只不透明的口袋中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后先从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.
(1)求摸出的2个球颜色相同的概率.
(2)活动设置了一等奖和二等奖两个奖次,一等奖的获奖率低于二等奖.现规定摸出颜色不同的两球和摸出颜色相同的两球分别对应不同奖次,请写出它们分别对应的奖次,并说明理由.
答案:解:(1)画树状图如下:
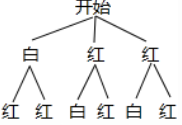
共有6种等可能出现的结果.所以摸出的2个球颜色相同的概率为$\frac {2}{6}=\frac {1}{3}。$
(2)摸出颜色不同的两球对应的奖次为二等奖,摸出颜色相同的两球分别对应的奖次为一等奖,
理由如下:由树状图可知,摸出颜色不同的两球的结果有4种,
摸出颜色相同的两球的结果有2种,
$\therefore $摸出颜色不同的两球的概率为$\frac {4}{6}=\frac {2}{3},$
摸出颜色相同的两球的概率为$\frac {2}{6}=\frac {1}{3},$
$\because $一等奖的获奖率低于二等奖,$\frac {1}{3} \lt \frac {2}{3},$
$\therefore $摸出颜色不同的两球对应的奖次为二等奖,
摸出颜色相同的两球分别对应的奖次为一等奖.