1. 选择题:
(1) 下列各组数中,不能作为直角三角形的三边长的是 (
C
)
A. 3,4,5
B. 10,6,8
C. 4,5,6
D. 12,13,5
(2) 三角形的三边长分别是 6,8,10,它最长边上的高是 (
B
)
A. 6
B. 4.8
C. 2.4
D. 8
(3) 在△ABC 中,AB= 13,AC= 15,边 BC 上的高 AD= 12,则 BC 的长为 (
C
)
A. 14
B. 4
C. 14 或 4
D. 以上都不对
答案:(1) C
(2) B
(3) C
解析:
(1) 对于选项A,$3^2 + 4^2 = 5^2$,满足勾股定理,故是直角三角形;
对于选项B,$6^2 + 8^2 = 10^2$,满足勾股定理,故是直角三角形;
对于选项C,$4^2 + 5^2 \neq 6^2$,不满足勾股定理,故不是直角三角形;
对于选项D,$5^2 + 12^2 = 13^2$,满足勾股定理,故是直角三角形。
所以不能作为直角三角形的三边长的是C选项。
(2) 已知三角形的三边长分别是6, 8, 10,根据勾股定理,$6^2 + 8^2 = 10^2$,所以这是一个直角三角形。
设最长边上的高为h,根据直角三角形的面积公式,$\frac{1}{2} × 6 × 8 = \frac{1}{2} × 10 × h$,解得$h = 4.8$。
(3) 在$\bigtriangleup ABC$中,已知$AB = 13$,$AC = 15$,边BC上的高$AD = 12$。
分两种情况考虑:
当$\bigtriangleup ABC$是锐角三角形时,利用勾股定理,$BD = \sqrt{AB^2 - AD^2} = 5$,$CD = \sqrt{AC^2 - AD^2} = 9$,所以$BC = BD + CD = 14$。
当$\bigtriangleup ABC$是钝角三角形时,利用勾股定理,$BD = \sqrt{AB^2 - AD^2} = 5$,$CD = \sqrt{AC^2 - AD^2} = 9$,但此时$BC = CD - BD = 4$。
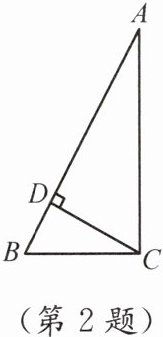
2. 如图,在△ABC 中,CD 是边 AB 上的高,AD= 9,BD= 1,CD= 3. △ABC 是直角三角形吗?为什么?
]
答案:是
因为$AD = 9$,$BD = 1$,所以$AB=AD + BD=9 + 1 = 10$。
在$Rt\triangle ACD$中,根据勾股定理$AC^{2}=AD^{2}+CD^{2}$,已知$AD = 9$,$CD = 3$,则$AC^{2}=9^{2}+3^{2}=81 + 9 = 90$。
在$Rt\triangle BCD$中,根据勾股定理$BC^{2}=BD^{2}+CD^{2}$,已知$BD = 1$,$CD = 3$,则$BC^{2}=1^{2}+3^{2}=1 + 9 = 10$。
$AC^{2}+BC^{2}=90 + 10 = 100$,而$AB^{2}=10^{2}=100$,所以$AC^{2}+BC^{2}=AB^{2}$。
根据勾股定理的逆定理,可知$\triangle ABC$是直角三角形,且$\angle C = 90^{\circ}$。
1. a,b,c 是△ABC 的三边,有以下四种情况:
① a= 5,b= 12,c= 13;
② a= 8,b= 15,c= 17;
③ a:b:c= 3:4:5;
④ a= 15,b= 20,c= 25.
其中,能说明△ABC 是直角三角形的有 (
D
)
A.1 个
B.2 个
C.3 个
D.4 个
答案:D
解析:
对于每一种情况,分别验证三边是否满足勾股定理的逆定理,即验证 $a^2 + b^2 = c^2$ 是否成立。
① 对于 $a=5, b=12, c=13$,有 $5^2 + 12^2 = 25 + 144 = 169 = 13^2$,满足条件,所以能构成直角三角形。
② 对于 $a=8, b=15, c=17$,有 $8^2 + 15^2 = 64 + 225 = 289 = 17^2$,满足条件,所以能构成直角三角形。
③ 对于 $a:b:c=3:4:5$,设 $a=3x, b=4x, c=5x$,则 $(3x)^2 + (4x)^2 = 9x^2 + 16x^2 = 25x^2 = (5x)^2$,满足条件,所以能构成直角三角形。
④ 对于 $a=15, b=20, c=25$,有 $15^2 + 20^2 = 225 + 400 = 625 = 25^2$,满足条件,所以能构成直角三角形。
综上,四种情况都能构成直角三角形。
2. 若正整数 a,b,c 满足方程$a^{2}+b^{2}= c^{2}$,则称这一组正整数(a,b,c)为“商高数”. 下面列举 5 组“商高数”:(3,4,5),(5,12,13),(6,8,10),(7,24,25),(12,16,20),注意这 5 组“商高数”的结构有如下规律:
$\left\{\begin{array}{l} 4= 2×2×1,\\ 3= 2^{2}-1^{2},\\ 5= 2^{2}+1^{2};\end{array} \right.$
$\left\{\begin{array}{l} 12= 2×3×2,\\ 5= 3^{2}-2^{2},\\ 13= 3^{2}+2^{2};\end{array} \right.$
$\left\{\begin{array}{l} 6= 2×3×1,\\ 8= 3^{2}-1^{2},\\ 10= 3^{2}+1^{2};\end{array} \right.$
$\left\{\begin{array}{l} 24= 2×4×3,\\ 7= 4^{2}-3^{2},\\ 25= 4^{2}+3^{2};\end{array} \right.$
$\left\{\begin{array}{l} 16= 2×4×2,\\ 12= 4^{2}-2^{2},\\ 20= 4^{2}+2^{2}.\end{array} \right.$
根据以上规律,回答以下问题:
(1) 写出各数都大于 30 的两组“商高数”;
(2) 用两个正整数 m,n(m>n)表示一组“商高数”,并证明你的结论.
答案:(1) 取m=7,n=4,得a=7²-4²=33,b=2×7×4=56,c=7²+4²=65,即(33,56,65);取m=8,n=5,得a=8²-5²=39,b=2×8×5=80,c=8²+5²=89,即(39,80,89)。
(2) 一组“商高数”可表示为(m²-n²,2mn,m²+n²),其中m,n为正整数且m>n。
证明:(m²-n²)²+(2mn)²=m⁴-2m²n²+n⁴+4m²n²=m⁴+2m²n²+n⁴=(m²+n²)²,即(m²-n²)²+(2mn)²=(m²+n²)²,故(m²-n²,2mn,m²+n²)是“商高数”。