活动一:读一读 试一试
说说可以用什么方法说明课本第 93 页图 3-9 中的三角形是直角三角形.
答案:通过测量角的度数或验证三边是否满足勾股定理的逆定理说明该三角形是直角三角形。
解析:
测量三角形三个角的度数,若有一个角为90°,则是直角三角形;或测量三角形三边长度,设三边长为a、b、c(c为最长边),验证是否满足a²+b²=c²,若满足则是直角三角形。
活动二:想一想 说一说
1. 一个三角形的三边满足什么条件时,这个三角形是直角三角形?
2. 如何说明三边长分别为 3 cm,4 cm,5 cm 的三角形是直角三角形?
3. 什么叫勾股数?你能用自己的语言概述吗?写出你所知道的勾股数.
4. 说说勾股定理与勾股定理的逆定理的联系与区别.
答案:1. 三边长满足$a^2 + b^2 = c^2$($c$为最长边);2. 因为$3^2 + 4^2 = 5^2$;3. 三个正整数,能构成直角三角形三边,如(3,4,5);4. 联系:均涉直角三角形边长关系,逆定理是勾股定理逆用;区别:勾股定理是性质定理,逆定理是判定定理。
解析:
1. 若三角形的三边长$a$、$b$、$c$满足$a^2 + b^2 = c^2$($c$为最长边),则这个三角形是直角三角形。
2. 因为$3^2 + 4^2 = 9 + 16 = 25 = 5^2$,满足勾股定理的逆定理条件,所以该三角形是直角三角形。
3. 能够成为直角三角形三条边长的三个正整数叫做勾股数。常见勾股数:(3,4,5)、(6,8,10)、(5,12,13)等。
4. 联系:两者都与直角三角形的边长关系有关,勾股定理的逆定理是勾股定理的逆用。区别:勾股定理是直角三角形的性质定理,已知直角三角形,得出三边关系;逆定理是直角三角形的判定定理,已知三边关系,判断是否为直角三角形。
活动三:想一想 做一做
1. 3,4,5 是一组勾股数,将这 3 个数分别扩大为原来的 2 倍,所得的 3 个数还是勾股数吗?扩大为原来的 3 倍、4 倍、k 倍(k 为正整数)呢?为什么?说说你的发现.
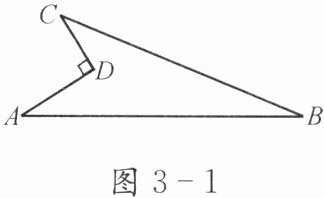
2. 如图 3-1,AD= 4,CD= 3,∠ADC= 90°,AB= 13,BC= 12. 求四边形 ABCD 的面积.
答案:1. 是勾股数,理由见解析;
2. $24$
解析:
1.
已知$3$,$4$,$5$是一组勾股数,因为$3^{2}+4^{2}=9 + 16=25=5^{2}$。
当将这$3$个数分别扩大为原来的$2$倍时,得到$6$,$8$,$10$,此时$6^{2}+8^{2}=36 + 64 = 100=10^{2}$,所以所得的$3$个数还是勾股数。
当扩大为原来的$3$倍时,得到$9$,$12$,$15$,$9^{2}+12^{2}=81+144 = 225=15^{2}$,是勾股数。
当扩大为原来的$4$倍时,得到$12$,$16$,$20$,$12^{2}+16^{2}=144 + 256=400=20^{2}$,是勾股数。
当扩大为原来的$k$倍($k$为正整数)时,得到$3k$,$4k$,$5k$,$(3k)^{2}+(4k)^{2}=9k^{2}+16k^{2}=25k^{2}=(5k)^{2}$,所以所得的$3$个数还是勾股数。
发现:勾股数扩大为原来的正整数倍后所得的$3$个数仍然是勾股数。
2.
在$Rt\triangle ADC$中,$AD = 4$,$CD = 3$,根据勾股定理$AC=\sqrt{AD^{2}+CD^{2}}=\sqrt{4^{2}+3^{2}}=\sqrt{16 + 9}=5$。
在$\triangle ABC$中,$AC = 5$,$BC = 12$,$AB = 13$,因为$5^{2}+12^{2}=25 + 144=169=13^{2}$,即$AC^{2}+BC^{2}=AB^{2}$,所以$\triangle ABC$是直角三角形,$\angle ACB = 90^{\circ}$。
四边形$ABCD$的面积$S = S_{\triangle ABC}-S_{\triangle ADC}$。
$S_{\triangle ABC}=\frac{1}{2}× AC× BC=\frac{1}{2}×5×12 = 30$,$S_{\triangle ADC}=\frac{1}{2}× AD× CD=\frac{1}{2}×4×3 = 6$。
所以$S = 30-6=24$。