1. 下列说法中,正确的是(
A
)
A.$\sqrt{2}-\sqrt{3}的相反数是\sqrt{3}-\sqrt{2}$
B.$\sqrt{2}-\sqrt{3}的绝对值是\sqrt{2}-\sqrt{3}$
C.$\sqrt{81}>9$
D.2 的倒数为$-\frac{1}{2}$
答案:A。
解析:
选项A:根据相反数的定义,一个数与它的相反数相加结果为0。所以,$\sqrt{2} - \sqrt{3}$的相反数应为$-(\sqrt{2} - \sqrt{3}) = \sqrt{3} - \sqrt{2}$,故A选项正确。
选项B:一个数的绝对值是该数与0的距离。由于$\sqrt{3} > \sqrt{2}$,所以$\sqrt{2} - \sqrt{3} < 0$,其绝对值应为$-\left(\sqrt{2} - \sqrt{3}\right) = \sqrt{3} - \sqrt{2}$,与B选项给出的$\sqrt{2} - \sqrt{3}$不符,故B选项错误。
选项C:根据平方根的定义,$\sqrt{81} = 9$,并不大于9,故C选项错误。
选项D:一个数的倒数是1除以该数。所以,2的倒数为$\frac{1}{2}$,与D选项给出的$-\frac{1}{2}$不符,故D选项错误。
2. 填空题:
(1)把下列各数填入相应的横线上:$-7$,$0.32$,$\frac{1}{3}$,$0$,$\sqrt{8}$,$\sqrt[3]{216}$,$-\frac{\pi}{2}$.
有理数集合:
$-7, 0.32, \frac{1}{3}, 0, \sqrt[3]{216}$
;无理数集合:
$\sqrt{8}, -\frac{\pi}{2}$
.
(2)若$\sqrt{y-1}+(x+2)^2= 0$,则$x+y= $
$-1$
.
(3)已知$a$,$b$都是无理数,且它们的和为 2,试写出一对符合要求的无理数$a$,$b$:
$1+\sqrt{2}$,$1-\sqrt{2}$(答案不唯一)
.
答案:(1) 有理数集合:${-7, 0.32, \frac{1}{3}, 0, \sqrt[3]{216}}$;无理数集合:${\sqrt{8}, -\frac{\pi}{2}}$。
(2) $-1$
(3) $1+\sqrt{2}$,$1-\sqrt{2}$(答案不唯一)
解析:
(1) 有理数是可以表示为两个整数的比的数,而无理数则不能表示为两个整数的比。
有理数集合:根据有理数的定义,$-7$ 是整数,因此是有理数;$0.32$ 是有限小数,因此也是有理数;$\frac{1}{3}$ 是两个整数的比,所以也是有理数;$0$ 是整数,因此也是有理数;$\sqrt[3]{216}$ 是 6,是整数,因此也是有理数。所以有理数集合为:${-7, 0.32, \frac{1}{3}, 0, \sqrt[3]{216}}$。
无理数集合:$\sqrt{8}$ 不能表示为两个整数的比,因此是无理数;$-\frac{\pi}{2}$,其中 $\pi$ 是一个无理数,所以 $-\frac{\pi}{2}$ 也是无理数。所以无理数集合为:${\sqrt{8}, -\frac{\pi}{2}}$。
(2) 由于 $\sqrt{y-1}$ 和 $(x+2)^2$ 都是非负数,且它们的和为 0,那么这两个数都必须为 0。
从 $\sqrt{y-1} = 0$ 可得 $y-1=0$,解得 $y=1$。
从 $(x+2)^2 = 0$ 可得 $x+2=0$,解得 $x=-2$。
所以 $x+y = -2+1 = -1$。
(3) 已知 $a$ 和 $b$ 都是无理数,且 $a+b=2$。
可以选择 $a = 1+\sqrt{2}$(无理数),那么 $b = 2 - a = 2 - (1+\sqrt{2}) = 1-\sqrt{2}$(也是无理数)。
所以一对符合要求的无理数 $a$ 和 $b$ 是 $1+\sqrt{2}$ 和 $1-\sqrt{2}$。
1. 已知$0<a<1$,在$a$,$\frac{1}{a}$,$\sqrt{a}$,$a^2$中,最大的是(
B
)
A.$a$
B.$\frac{1}{a}$
C.$\sqrt{a}$
D.$a^2$
答案:B
解析:
1. 首先,我们已知$0 < a < 1$。
2. 对于$a^2$,由于$0 < a < 1$,那么$a^2$会比$a$更小,即$a^2 < a$。
3. 对于$\sqrt{a}$,由于$0 < a < 1$,开方后仍然保持在这个范围内,即$a < \sqrt{a} < 1$。
4. 对于$\frac{1}{a}$,由于$0 < a < 1$,当$a$趋近于0时,$\frac{1}{a}$会趋近于无穷大,因此$\frac{1}{a} > 1$。
5. 综合以上分析,我们可以得出:$a^2 < a < \sqrt{a} < 1 < \frac{1}{a}$。
2. 一个实数的绝对值是$\sqrt{7}-\sqrt{3}$,这个实数是
$\pm(\sqrt{7} - \sqrt{3})$
.
答案:$\pm(\sqrt{7} - \sqrt{3})$
解析:
设这个实数为$x$,根据绝对值的定义,有:
$|x| = \sqrt{7} - \sqrt{3}$
这意味着$x$可以是$\sqrt{7} - \sqrt{3}$或$-(\sqrt{7} - \sqrt{3})$。
即:
$x = \sqrt{7} - \sqrt{3} \quad 或 \quad x = -(\sqrt{7} - \sqrt{3}) = \sqrt{3} - \sqrt{7}$
3. 在如图所示的数轴上,点 C 与点 B 关于点 A 对称,C,A 两点对应的实数分别是$\sqrt{5}$和 1,则点 B 对应的实数为
$2 - \sqrt{5}$
.
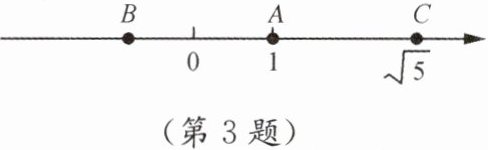
答案:$2 - \sqrt{5}$
解析:
点$C$和点$B$关于点$A$对称,$C$、$A$两点对应的实数分别是$\sqrt{5}$和$1$。
设点$B$对应的实数为$x$。
根据对称性质,点$A$到点$B$的距离等于点$A$到点$C$的距离,
即$|1 - x| = |\sqrt{5} - 1|$。
由于$x$在点$A$左侧,
所以$1 - x = \sqrt{5} - 1$,
解得$x = 2 - \sqrt{5}$。
4. 比较下列各组数的大小,并用计算器验证:
(1)$\sqrt{5}与\frac{1}{\sqrt{2}}$;
(2)$\sqrt[3]{7}与\sqrt{7}$;
(3)$\sqrt{0.16}与\frac{1}{\sqrt{0.16}}$.
答案:(1)
首先,将$\frac{1}{\sqrt{2}}$转化为有理化的形式:
$\frac{1}{\sqrt{2}} = \frac{1 × \sqrt{2}}{\sqrt{2} × \sqrt{2}} = \frac{\sqrt{2}}{2}$
由于 $\sqrt{5} > \sqrt{2}$,且$\sqrt{2} > \frac{\sqrt{2}}{2}$,
所以 $\sqrt{5} > \frac{1}{\sqrt{2}}$。
用计算器验证:
$\sqrt{5} \approx 2.236$
$\frac{1}{\sqrt{2}} \approx 0.707$
所以 $\sqrt{5} > \frac{1}{\sqrt{2}}$。
(2)
首先,求两数的6次方:
$(\sqrt[3]{7})^{6} = 7^{2} = 49$
$(\sqrt{7})^{6} = 7^{3} = 343$
由于 $49 < 343$,
所以 $\sqrt[3]{7} < \sqrt{7}$。
用计算器验证:
$\sqrt[3]{7} \approx 1.913$
$\sqrt{7} \approx 2.646$
所以 $\sqrt[3]{7} < \sqrt{7}$。
(3)
首先,计算$\sqrt{0.16}$的值:
$\sqrt{0.16} = 0.4$
再计算$\frac{1}{\sqrt{0.16}}$的值:
$\frac{1}{\sqrt{0.16}} = \frac{1}{0.4} = 2.5$
由于 $0.4 < 2.5$,
所以 $\sqrt{0.16} < \frac{1}{\sqrt{0.16}}$。
用计算器验证:
$\sqrt{0.16} = 0.4$
$\frac{1}{\sqrt{0.16}} = 2.5$
所以 $\sqrt{0.16} < \frac{1}{\sqrt{0.16}}$。
5. 计算:
(1)$\sqrt{(-2)^2}+|\sqrt{2}-1|-(\sqrt{2}-1)$;
(2)$|\sqrt{5}-\sqrt{2}|-(3+\sqrt{5})+(\sqrt{2}-2)^0$.
答案:(1)
解:
首先计算平方根:$\sqrt{(-2)^2} = \sqrt{4} = 2$
接着计算绝对值:$|\sqrt{2}-1| = \sqrt{2}-1$ (因为 $\sqrt{2} > 1$)
最后进行加减运算:
$\sqrt{(-2)^2}+|\sqrt{2}-1|-(\sqrt{2}-1) = 2 + (\sqrt{2}-1) - (\sqrt{2}-1) = 2$
(2)
解:
首先计算绝对值:$|\sqrt{5}-\sqrt{2}| = \sqrt{5}-\sqrt{2}$ (因为 $\sqrt{5} > \sqrt{2}$)
接着计算零指数幂:$(\sqrt{2}-2)^0 = 1$
最后进行加减运算:
$|\sqrt{5}-\sqrt{2}|-(3+\sqrt{5})+(\sqrt{2}-2)^0 = (\sqrt{5}-\sqrt{2}) - (3+\sqrt{5}) + 1 = -\sqrt{2} - 2$
6. 将图中的纸片剪拼成一个正方形(先剪成若干块,再将它们拼在一起,要求拼接时无空隙且不重叠).

答案:1. 计算原图面积:将图形分割为边长2的正方形和边长1的正方形,面积为$2^2 + 1^2 = 5$,故正方形边长为$\sqrt{5}$。
2. 剪切:连接原图左下角顶点与右侧竖边中点(坐标(2,1)),沿此线段剪开,得到一直角三角形(直角边1和2,斜边$\sqrt{5}$)和一四边形。
3. 拼接:将直角三角形绕斜边端点旋转180°,与四边形拼接,使斜边重合,各边对应,形成边长为$\sqrt{5}$的正方形。