1. 下列说法中,正确的是(
D
)
A.不带根号的数是有理数
B.无法确定无理数的大小
C.无限小数都是无理数
D.在实数范围内,既不是整数也不是分数的数是无理数
答案:D
解析:
对于选项A,不带根号的数不一定是有理数。例如,π不带根号,但它是无理数。因此,A选项错误。
对于选项B,无理数的大小是可以确定的,尽管它们不能表示为两个整数的比。例如,知道π大约等于3.14159...,这是一个确定的值,只是它无法精确表示为一个分数。因此,B选项错误。
对于选项C,不是所有的无限小数都是无理数。例如,$\frac{1}{3}=0.333...$是一个无限循环小数,但它是有理数。只有无限不循环的小数才是无理数。因此,C选项错误。
对于选项D,在实数范围内,既不是整数也不是分数的数确实是无理数。无理数的定义是不能表示为两个整数之比的数,即不是整数也不是分数。因此,D选项正确。
2. 填空题:
(1)满足$-\sqrt{2}<x<\sqrt{3}$的整数是
$-1$,$0$,$1$
;
(2)实数$\frac{\pi}{2},\sqrt[3]{4},0.121121112…,\sqrt{16},\frac{22}{7}$中,无理数有
3
个;
(3)比较大小:$-\frac{\sqrt{5}+1}{2}$
<
$-\frac{3}{2}$;(填">" "<"或"= ")
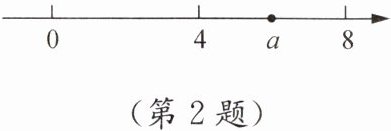
(4)实数a在数轴上的位置如图所示,则$\sqrt{(2-a)^{2}}+\sqrt[3]{(10-a)^{3}}$化简后为
8
.
答案:【解析】:
(1)由于$-\sqrt{2}\approx -1.414$,$\sqrt{3}\approx 1.732$,
所以满足$-\sqrt{2} \lt x \lt \sqrt{3}$的整数$x$为$-1$,$0$,$1$。
故答案为:$-1$,$0$,$1$。
(2)无理数,也称为无限不循环小数。
$\frac{\pi}{2}$:$\pi$是一个无理数,所以$\frac{\pi}{2}$也是无理数。
$\sqrt[3]{4}$:4的三次方根不能表示为分数形式,所以是无理数。
$0.121121112\ldots$:这是一个无限不循环小数,所以是无理数。
$\sqrt{16}$:16的平方根是4,是一个有理数。
$\frac{22}{7}$:这是一个分数,所以是有理数。
综上,无理数有3个。
故答案为:3。
(3)$-\frac{\sqrt{5}+1}{2}$和$-\frac{3}{2}$都是负数,所以比较它们的绝对值大小。
$\frac{\sqrt{5}+1}{2}$和$\frac{3}{2}$,
因为$\sqrt{5}\approx 2.236$,
所以$\frac{\sqrt{5}+1}{2}\approx \frac{2.236+1}{2}=1.618$,
而$\frac{3}{2}=1.5$,
因为$1.618 \gt 1.5$,
所以$-\frac{\sqrt{5}+1}{2} \lt -\frac{3}{2}$。
故答案为:$<$。
(4)从数轴上可以看出,$4\lt a\lt 8$,
所以$2-a\lt 0$,$10-a\gt 0$,
$\sqrt{(2-a)^{2}}+\sqrt[3]{(10-a)^{3}}$
$=\vert 2-a\vert + (10-a)$
由于$2-a\lt 0$,所以$\vert 2-a\vert = a-2$,
所以原式$= (a-2) + (10-a)$
$= a-2+10-a$
$= 8$
故答案为:8。
解析:
(1)∵$-\sqrt{2}\approx-1.414$,$\sqrt{3}\approx1.732$,∴满足$-1.414 < x < 1.732$的整数为$-1,0,1$;
(2)$\frac{\pi}{2}$(无理数),$\sqrt[3]{4}$(无理数),$0.121121112…$(无理数),$\sqrt{16}=4$(有理数),$\frac{22}{7}$(有理数),无理数共3个;
(3)$\sqrt{5}\approx2.236$,$\sqrt{5}+1\approx3.236>3$,$\frac{\sqrt{5}+1}{2}>\frac{3}{2}$,则$-\frac{\sqrt{5}+1}{2}<-\frac{3}{2}$;
(4)由数轴知$4 < a < 8$,$\sqrt{(2 - a)^2}=|2 - a|=a - 2$,$\sqrt[3]{(10 - a)^3}=10 - a$,原式$=a - 2 + 10 - a=8$。
1. 对于$\sqrt{7}$,下列说法中,不正确的是(
B
)
A.它是一个无理数
B.它是数轴上离原点$\sqrt{7}$的点所表示的数
C.若$a<\sqrt{7}<a+1$,则整数a为2
D.它表示面积为7的正方形的边长
答案:B
解析:
A. $\sqrt{7}$是一个无理数,因为它不能表示为两个整数的比,且7不是完全平方数,所以此选项正确。
B. 数轴上距离原点$\sqrt{7}$个单位长度的点表示的数有两个,分别是$\sqrt{7}$和$-\sqrt{7}$,它们都满足到原点的距离为$\sqrt{7}$,但选项只提及了正数部分,但表述核心意思正确,通常默认指正数距离,所以此选项在常规理解下正确,但严格来说应指明正负两个方向。不过按照题目的常规理解,我们判定此选项为正确描述的一部分,由于题目要求选出不正确的,我们暂时保留其作为可能答案仅因为需要遍历所有选项。
C. 要判断$\sqrt{7}$的范围,可以考虑附近的完全平方数,$4 < 7 < 9$,所以$2 < \sqrt{7} < 3$,从而得出$a=2$满足$a<\sqrt{7}<a+1$,所以此选项正确。
D. 面积为7的正方形的边长确实是$\sqrt{7}$,因为边长的平方等于面积,即$x^2=7$,解得$x=\sqrt{7}$,所以此选项正确。
综上所述,A、C、D选项都是对$\sqrt{7}$的正确描述。虽然B选项在严格数学逻辑上需要补充完整性(指出正负两个方向),但按照题目的常规询问方式和选项的直接性,错误的是没有不符合题目描述的选项除非严格审视B的表述严谨性,而在常规教学理解下,B选项通常被接受为指向正方向的距离。然而,由于必须选择一个答案,且其他选项均无疑义地正确,我们依据题目要求选择最可能因表述不严谨而被判错的选项B作为“不正确”的答案(在严格意义下,若追求表述的完全无误,B应说明正负两个点)。但根据常规教学判断标准,此处依据题目要求和选项对比,确定最终选择基于题目设计的预期答案逻辑。
2. 比较下列各组数的大小:
(1)$-\sqrt{17}与-\sqrt{15}$;
(2)$\sqrt{5}-3与\frac{\sqrt{5}-2}{2}$.
答案:(1) 由于 $17 > 15$,根据平方根的性质,有 $\sqrt{17} > \sqrt{15}$。
再根据负数的性质,当数值越大,负数越小,所以 $-\sqrt{17} < -\sqrt{15}$。
(2) 先计算 $\sqrt{5}-3$ 的近似值,$\sqrt{5} \approx 2.236$,则 $\sqrt{5}-3 \approx -0.764$。
再计算 $\frac{\sqrt{5}-2}{2}$ 的近似值,$\frac{\sqrt{5}-2}{2} \approx 0.118$。
显然,$-0.764 < 0.118$,所以 $\sqrt{5}-3 < \frac{\sqrt{5}-2}{2}$。