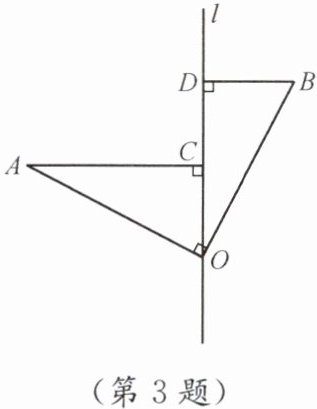
3. 如图,∠AOB= 90°,OA= OB,直线 l 经过点 O,分别过点 A,B 作 AC⊥l,BD⊥l,垂足分别为 C,D.求证:OC= BD.
答案:证明:
因为$\angle AOB = 90^\circ$,
所以$\angle AOC + \angle BOD = 90^\circ$。
因为$AC \perp l$,$BD \perp l$,
所以$\angle ACO = \angle BDO = 90^\circ$。
因为$\angle ACO = 90^\circ$,
所以$\angle A + \angle AOC = 90^\circ$。
又因为$\angle AOC + \angle BOD = 90^\circ$,
所以$\angle A = \angle BOD$。
在$\triangle ACO$和$\triangle ODB$中,
$\begin{aligned}\angle ACO &= \angle ODB,\\\angle A &= \angle BOD,\\OA&=OB.\end{aligned}$
所以$\triangle ACO \cong \triangle ODB (AAS)$,
所以$OC = BD$。
4. 如图,已知点 A,F,E,C 在一条直线上,AB//CD,∠ABE= ∠CDF,AF= CE.
(1)从图中任意找两组全等三角形;
(2)从第(1)题中所找的全等三角形中任选一组进行证明.

答案:(1) △ABE≌△CDF,△ADF≌△CBE
(2) 证明△ABE≌△CDF:
∵AB//CD,∴∠BAE=∠DCF(两直线平行,内错角相等).
∵AF=CE,∴AF+FE=CE+FE,即AE=CF.
在△ABE和△CDF中,
∠ABE=∠CDF(已知),
∠BAE=∠DCF(已证),
AE=CF(已证),
∴△ABE≌△CDF(AAS).
在△ABC 中,∠ACB= 90°,AC= BC,动直线 MN 经过点 C,且 AD⊥MN,BE⊥MN,垂足分别为 D,E.
(1)若直线 MN 在图①位置,① 求证:△ADC≌△CEB;② 求证:DE= AD+BE.
(2)若直线 MN 绕点 C 旋转到图②位置,求证:DE= AD-BE.
(3)若直线 MN 绕点 C 旋转到图③位置,DE,AD,BE 之间有怎样的等量关系?请直接写出这个等量关系.

答案:(1)①证明:
因为$AD\perp MN$,$BE\perp MN$,$\angle ACB = 90^{\circ}$,
所以$\angle ADC=\angle CEB = 90^{\circ}$,$\angle ACD+\angle BCE = 90^{\circ}$,$\angle ACD+\angle CAD = 90^{\circ}$,
则$\angle CAD=\angle BCE$。
又$AC = BC$,
所以$\triangle ADC\cong\triangle CEB(AAS)$。
②证明:
由①知$\triangle ADC\cong\triangle CEB$,
所以$AD = CE$,$CD = BE$,
则$DE=CD + CE=AD + BE$。
(2)证明:
因为$AD\perp MN$,$BE\perp MN$,$\angle ACB = 90^{\circ}$,
所以$\angle ADC=\angle CEB = 90^{\circ}$,$\angle ACD+\angle BCE = 90^{\circ}$,$\angle BCE+\angle CBE = 90^{\circ}$,
则$\angle ACD=\angle CBE$。
又$AC = BC$,
所以$\triangle ADC\cong\triangle CEB(AAS)$。
所以$AD = CE$,$CD = BE$,
则$DE=CE - CD=AD - BE$。
(3)$DE=BE - AD$。