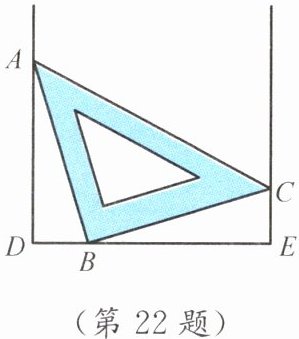
22.(12分)如图,把一块三角尺(AB= BC,∠ABC= 90°)放入一个“U”形槽中,使三角尺的三个顶点A,B,C分别在槽的两壁及底边上滑动,已知∠D= ∠E= 90°.在滑动过程中,你发现线段AD与BE有什么关系?试说明你的结论.
答案:AD=BE且AD//BE。
证明:
∵∠D=∠E=90°,
∴AD⊥DE,BE⊥DE,故∠ADB=∠BEC=90°,AD//BE(垂直于同一直线的两直线平行)。
∵∠ABC=90°,
∴∠ABD+∠CBE=90°。
在Rt△ABD中,∠ABD+∠BAD=90°,
∴∠BAD=∠CBE(同角的余角相等)。
在△ABD和△BCE中,
∠ADB=∠BEC=90°,
∠BAD=∠CBE,
AB=BC,
∴△ABD≌△BCE(AAS),
∴AD=BE。
综上,AD=BE且AD//BE。
23.(10分)如图,在△ABC中,点D在边AC上,DB= BC,E是CD的中点,F是AB的中点.求证:$EF= \frac{1}{2}AB$.

答案:证明:
连接$BE$。
$\because DB=BC$,$E$是$CD$的中点,
$\therefore BE\perp CD$,
$\therefore \angle AEB=90^\circ$。
$\because F$是$AB$的中点,
$\therefore EF=\frac{1}{2}AB$(直角三角形斜边中线等于斜边的一半)。
24.(12分)如图①,△ABC是等边三角形,△BDC是等腰三角形,BD= CD,∠BDC= 120°,以D为顶点作一个60°角,角的两边分别与边AB,AC交于点M,N,连接MN.
(1)探究BM,MN,NC之间的数量关系,并说明理由;
(2)若△ABC的边长为2,求△AMN的周长;
(3)若点M,N分别在AB,CA的延长线上,其他条件不变,在图②中画出图形,并说出BM,MN,NC之间的数量关系.

答案:(1) $BM + NC = MN$
延长 $AC$ 至 $E$,使得 $CE = BM$,连接 $DE$。
因为 $\triangle ABC$ 是等边三角形,$\triangle BDC$ 是等腰三角形,$\angle BDC = 120^{\circ}$,
所以 $\angle ABC = \angle ACB = 60^{\circ}$,$\angle DBC = \angle DCB = 30^{\circ}$,
则 $\angle ABD = \angle ACD = 90^{\circ}$。
在 $\triangle BDM$ 和 $\triangle CDE$ 中,
$BD = CD$,$\angle DBM = \angle DCE = 90^{\circ}$,$BM = CE$,
所以 $\triangle BDM \cong \triangle CDE(SAS)$,
所以 $DM = DE$,$\angle BDM = \angle CDE$。
因为 $\angle BDC = 120^{\circ}$,$\angle MDN = 60^{\circ}$,
所以 $\angle BDM + \angle NDC = \angle CDE + \angle NDC = \angle BDC - \angle MDN = 60^{\circ}$,
即 $\angle MDN = \angle NDE = 60^{\circ}$。
在 $\triangle MDN$ 和 $\triangle EDN$ 中,
$DM = DE$,$\angle MDN = \angle EDN$,$DN = DN$,
所以 $\triangle MDN \cong \triangle EDN(SAS)$,
所以 $MN = EN$,
又因为 $EN = NC + CE$,$CE = BM$,
所以 $BM + NC = MN$。
(2) 由(1)知 $BM + NC = MN$,
所以 $\triangle AMN$ 的周长为 $AM + AN + MN = AM + AN + BM + NC = AB + AC$,
因为 $\triangle ABC$ 的边长为 $2$,
所以 $\triangle AMN$ 的周长为 $2 + 2 = 4$。
(3) 图形:在 $AB$ 的延长线上取点 $M$,在 $CA$ 的延长线上取点 $N$,连接 $MN$,$\angle MDN = 60^{\circ}$。
$MN = BM - NC$
在 $AB$ 上截取 $BF = CN$,连接 $DF$。
因为 $\angle ABD = \angle ACD = 90^{\circ}$,$BD = CD$,$\angle BDC = 120^{\circ}$,
在 $\triangle BDF$ 和 $\triangle CDN$ 中,
$BD = CD$,$\angle DBF = \angle DCN = 90^{\circ}$,$BF = CN$,
所以 $\triangle BDF \cong \triangle CDN(SAS)$,
所以 $DF = DN$,$\angle BDF = \angle CDN$。
因为 $\angle BDC = 120^{\circ}$,$\angle MDN = 60^{\circ}$,
所以 $\angle BDF + \angle MDC = \angle CDN + \angle MDC = \angle BDC - \angle MDN = 60^{\circ}$,
即 $\angle FDM = \angle MDN = 60^{\circ}$。
在 $\triangle FDM$ 和 $\triangle NDM$ 中,
$DF = DN$,$\angle FDM = \angle NDM$,$DM = DM$,
所以 $\triangle FDM \cong \triangle NDM(SAS)$,
所以 $MN = FM$,
又因为 $FM = BM - BF$,$BF = CN$,
所以 $MN = BM - NC$。