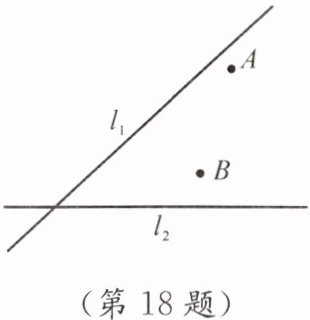
18.(8分)如图,现有两条高速公路$l_1$,$l_2$和两个城镇A,B.准备建一个燃气控制中心站P,使中心站到两条公路的距离相等,并且到两个城镇等距离,请你画出中心站的位置(不写作法,保留作图痕迹).
答案:(作图痕迹如下:)
1. 作直线$l_1$与$l_2$相交所成角的平分线(两条);
2. 作线段$AB$的垂直平分线;
3. 上述角平分线与垂直平分线的交点即为点$P$。
(注:实际答题需在图中保留角平分线和垂直平分线的作图痕迹,标出交点$P$。)
19.(10分)如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件:
$AE=AF$(答案不唯一)
.试证明.

答案:$AE=AF$(答案不唯一)。
证明:
因为$AD$是$\triangle ABC$的角平分线,
所以$\angle EAD=\angle FAD$,
在$\triangle AED$和$\triangle AFD$中,
$\begin{cases}AE = AF,\\\angle EAD=\angle FAD,\\AD = AD.\end{cases}$
所以$\triangle AED\cong\triangle AFD(SAS)$。
20.(10分)如图,点C,E分别在直线AB,DF上,CF和BE相交于点O,CO= FO,EO= BO.若∠ACE= 70°,求∠DEC的度数.

答案:在$\triangle COB$和$\triangle FOE$中,
$\begin{cases}CO = FO,\\\angle COB=\angle FOE ,\\BO = EO.\end{cases}$
所以$\triangle COB\cong\triangle FOE(SAS)$。
所以$\angle OCB=\angle OFE$。
因为$AB// DF$,所以$\angle OCB=\angle OFE=\angle DFC$ ,两直线平行,内错角相等。
已知$\angle ACE = 70^{\circ}$,则$\angle OCB = 180^{\circ}-\angle ACE=180^{\circ}- 70^{\circ}=110^{\circ}$。
所以$\angle DFC=\angle OCB = 110^{\circ}$。
根据平角为$180^{\circ}$,可得$\angle DEC = 180^{\circ}-\angle DFC=180^{\circ}-110^{\circ}=70^{\circ}$。
综上,$\angle DEC$的度数为$70^{\circ}$。
21.(10分)如图,∠AOB= 90°,OA= 45 cm,OB= 15 cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

答案:设机器人行走的路程$BC = x\ cm$。
因为小球滚动速度与机器人行走速度相等,且运动时间相同,所以小球滚动的路程$AC = BC = x\ cm$。
已知$OA = 45\ cm$,则$OC = OA - AC = (45 - x)\ cm$。
在$Rt\triangle OBC$中,$\angle AOB = 90^\circ$,$OB = 15\ cm$,由勾股定理得:
$OB^2 + OC^2 = BC^2$
即:
$15^2 + (45 - x)^2 = x^2$
展开并化简:
$225 + 2025 - 90x + x^2 = x^2$
$2250 - 90x = 0$
解得:
$x = 25$
答:机器人行走的路程$BC$是$25\ cm$。