1. 下列图象中,以方程 $ y - 2x - 2 = 0 $ 的解为坐标的点组成的图象是(
C
)
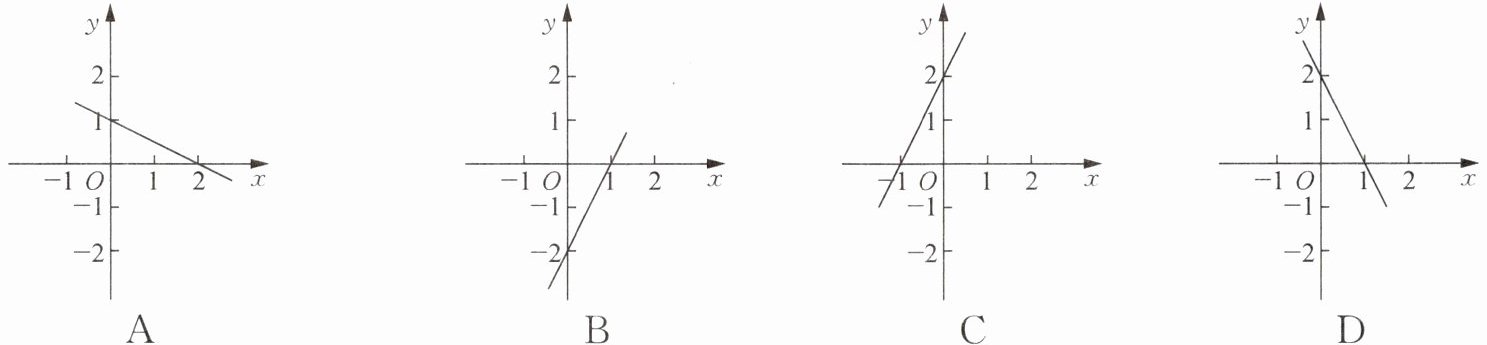
答案:C
解析:
方程$y - 2x - 2 = 0$可化为$y = 2x + 2$,此为一次函数,斜率为2(正,函数单调递增),截距为2(与y轴交于(0,2))。选项C的图象符合斜率为正且过(0,2),故C正确。
2. 一次函数 $ y = 3x - 2 $ 和 $ y = -2x + 3 $ 图象的交点坐标是(
A
)
A.(1,1)
B.(1,-1)
C.(-1,1)
D.(-1,-1)
答案:A
解析:
要求两个一次函数图象的交点,需要联立两个一次函数的解析式,求解方程组。
联立方程组:
$\begin{cases}y = 3x - 2, \\y = -2x + 3.\end{cases}$
由于两个方程的$y$值相等,可以得到:
$3x - 2 = -2x + 3$,
移项并合并同类项:
$5x = 5$,
解得:
$x = 1$,
将$x = 1$代入任一方程中求解$y$值,例如代入第一个方程:
$y = 3 × 1 - 2 = 1$,
所以,两个一次函数图象的交点坐标为$(1, 1)$。
3. 若一次函数 $ y = -\frac{1}{2}x - 2 $ 与 $ y = 2x - 7 $ 的图象交点为 (2,-3),则二元一次方程组 $ \begin{cases} x + 2y = -4, \\ 2x - y = 7 \end{cases} $ 的解为
(2,-3)
.
答案:(2,-3)
解析:
已知一次函数 $ y = -\frac{1}{2}x - 2 $ 和 $ y = 2x - 7 $ 的交点为 (2, -3),即当 $ x = 2 $ 时,$ y = -3 $。
将 $ x = 2 $ 和 $ y = -3 $ 代入方程组 $ \begin{cases} x + 2y = -4, \\ 2x - y = 7 \end{cases} $ 进行验证:
1. 代入第一个方程 $ x + 2y = -4 $:
$ 2 + 2(-3) = 2 - 6 = -4 $
满足方程。
2. 代入第二个方程 $ 2x - y = 7 $:
$ 2(2) - (-3) = 4 + 3 = 7 $
满足方程。
因此,方程组的解为 $ x = 2 $,$ y = -3 $。
4. (1)在如图所示的平面直角坐标系中,利用图象法解二元一次方程组 $ \begin{cases} x + y = 4, \\ 2x - y = -1. \end{cases} $
(2)求第(1)题中图象与 x 轴所围成的三角形的面积.

答案:(1)将$x+y=4$转化为$y=-x+4$,当$x=0$时,$y=4$;当$y=0$时,$x=4$,过点$(0,4)$和$(4,0)$画直线。
将$2x-y=-1$转化为$y=2x+1$,当$x=0$时,$y=1$;当$y=0$时,$x=-\frac{1}{2}$,过点$(0,1)$和$(-\frac{1}{2},0)$画直线。
两条直线的交点为$(1,3)$,所以方程组的解为$\begin{cases}x=1,\\y=3.\end{cases}$
(2)由(1)可知,直线$x+y=4$与$x$轴交点为$(4,0)$,直线$2x-y=-1$与$x$轴交点为$(-\frac{1}{2},0)$,交点坐标为$(1,3)$。
围成的三角形以$\vert4-(-\frac{1}{2})\vert=\frac{9}{2}$为底,交点的纵坐标的绝对值$3$为高。
根据三角形面积公式$S=\frac{1}{2}×底×高$,可得$S=\frac{1}{2}×\frac{9}{2}×3=\frac{27}{4}$。
解析:
(1)对于方程$x + y = 4$,当$x = 0$时,$y = 4$;当$y = 0$时,$x = 4$,过点$(0,4)$、$(4,0)$作直线。对于方程$2x - y = -1$,当$x = 0$时,$y = 1$;当$y = 0$时,$x=-\frac{1}{2}$,过点$(0,1)$、$(-\frac{1}{2},0)$作直线。两直线交点坐标为$(1,3)$,所以方程组的解为$\begin{cases} x = 1 \\ y = 3 \end{cases}$。
(2)由
(1)知两直线与$x$轴交点分别为$(4,0)$、$(-\frac{1}{2},0)$,两交点之间的距离为$4 - (-\frac{1}{2})=\frac{9}{2}$。两直线交点$(1,3)$到$x$轴的距离为$3$,所以所围成三角形的面积为$\frac{1}{2}×\frac{9}{2}×3=\frac{27}{4}$。
1. 用图象法解某二元一次方程组时,在同一平面直角坐标系中作出的相应两个一次函数的图象(如图).该二元一次方程组是(
C
)

A.$ \begin{cases} y = 2x + 1, \\ y = x + 2 \end{cases} $
B.$ \begin{cases} y = 3x + 1, \\ y = x - 5 \end{cases} $
C.$ \begin{cases} y = -2x + 1, \\ y = x - 1 \end{cases} $
D.$ \begin{cases} y = -x + 3, \\ y = 3x - 5 \end{cases} $
答案:C
解析:
根据图象,两条直线相交于点$(2, -1)$。
将点$(2, -1)$代入各选项验证:
A.$y = 2x + 1$,$y = x + 2$,
当$x = 2$时,$y = 2× 2 + 1 = 5\neq -1$,$y = 2 + 2 = 4\neq -1$,不符合。
B.$y = 3x + 1$,$y = x - 5$,
当$x = 2$时,$y = 3× 2 + 1 = 7\neq -1$,$y = 2 - 5 = -3\neq -1$,不符合。
C.$y = -2x + 1$,$y = x - 1$,
当$x = 2$时,$y = -2× 2 + 1 = -3\neq -1$,$y = 2 - 1 = 1\neq -1$,但看斜率,$l_1$斜率为负,$l_2$斜率为正,且从图象看,$l_1$:当$x = 0$时,$y = 1$,$l_1$:$y = -2x + 1$;$l_2$:当$x = 0$时,$y = -1$,且$y = x - 1$经过$(2, -1)$,符合图象。
D.$y = -x + 3$,$y = 3x - 5$,
当$x = 2$时,$y = -2 + 3 = 1\neq -1$,$y = 3× 2 - 5 = 1\neq -1$,不符合。
从图象可知,$l_1$过点$(0,1)$和$(2, -1)$,斜率$k_1=\frac{-1 - 1}{2 - 0}=-1$,$l_2$过点$(0, -1)$和$(2, -1)$,斜率$k_2=\frac{-1+1}{2 - 0}=1$,$l_1$:$y=-x + 1$(这里根据两点式求出),$l_2$:$y = x-1$,最符合的是C选项中两个函数图象的特征。
2. 已知一次函数 $ y = ax + 2 $ 与 $ y = kx + b $ 的图象如图所示,且方程组 $ \begin{cases} y = ax + 2, \\ y = kx + b \end{cases} $ 的解为 $ \begin{cases} x = 2, \\ y = 1 \end{cases} $,点 B 的坐标为 (0,-1),P 是 y 轴上的一个动点.若 $ S_{\triangle ABP} = 6 $,则点 P 的坐标为
$(0,5)$或$(0,-7)$
.

答案:$(0,5)$或$(0,-7)$
解析:
∵方程组$\begin{cases} y=ax+2 \\ y=kx+b \end{cases}$的解为$\begin{cases} x=2 \\ y=1 \end{cases}$,∴两函数图象交点$A(2,1)$。
∵点$B(0,-1)$,$P$是$y$轴上动点,设$P(0,p)$。
$B$、$P$在$y$轴上,$BP$长为$|p - (-1)| = |p + 1|$,点$A$到$y$轴距离为$2$(即横坐标绝对值)。
$S_{\triangle ABP}=\frac{1}{2} × BP × 2 = |p + 1|$,由$S_{\triangle ABP}=6$得$|p + 1|=6$。
解得$p=5$或$p=-7$,∴$P(0,5)$或$(0,-7)$。