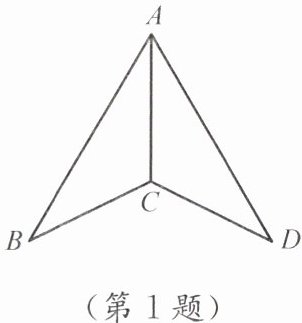
1. 如图,AB= AD,若要用“SAS”说明△ABC≌△ADC,则需要添加的条件是
∠BAC=∠DAC
.
答案:∠BAC=∠DAC
解析:
根据“SAS”(边-角-边)判定定理,需要两个三角形有两条边和它们夹角对应相等。
已知AB=AD,且AC是公共边,即AC=AC。
因此,为了满足“SAS”定理,需要添加的条件是∠BAC=∠DAC。
2. 在△ABC 和△FED 中,已知∠A= ∠F,AC= FD,要根据“SAS”说明这两个三角形全等,还需要添加的条件是(
C
)
A.AB= DE
B.BC= EF
C.AB= FE
D.∠C= ∠D
答案:C
解析:
已知在△ABC和△FED中,∠A=∠F,AC=FD。
根据“SAS”(边角边)全等条件,需要两组对应边相等,并且这两组对应边所夹的角相等。
在这里,已经有一组对应边AC和FD相等,以及它们所夹的角∠A和∠F相等。
因此,还需要另一组对应边相等。
观察选项,AB和FE是另一组可能的对应边。
如果AB=FE,那么结合已知的AC=FD和∠A=∠F,就可以根据“SAS”判定△ABC和△FED全等。
而AB和DE不是对应边,BC和EF也不是对应边,∠C和∠D是对应角,但“SAS”需要的是对应边。
3. 能判定△ABC≌△DEF 的条件是(
D
)
A.AB= DE,AC= DF,∠C= ∠F
B.AB= DE,∠A= ∠D,BC= EF
C.AC= DF,∠A= ∠D,BC= EF
D.AC= DF,∠C= ∠F,BC= EF
答案:D
解析:
A选项中AB=DE,AC=DF,∠C=∠F,∠C和∠F并不是这两组边的夹角,所以不能根据SAS判定全等。
B选项中AB=DE,∠A=∠D,BC=EF,BC和EF并不是∠A和∠D的夹边,所以不能根据SAS判定全等。
C选项中AC=DF,∠A=∠D,BC=EF,同样不满足全等三角形的判定条件。
D选项中AC=DF,∠C=∠F,BC=EF,满足两边及其夹角对应相等,即SAS全等条件,所以能判定$\triangle ABC\cong\triangle DEF$。
4. 已知:如图,O 分别是 AB,CD 的中点,AB,CD 相交于点 O.
求证:△AOC≌△BOD.

答案:证明:
∵O是AB中点,
∴AO=BO。
∵O是CD中点,
∴CO=DO。
在△AOC和△BOD中,
∠AOC=∠BOD(对顶角相等),
AO=BO,
CO=DO,
∴△AOC≌△BOD(SAS)。
5. 如图,在△ABC 中,AB= AC,AD 平分∠BAC.
(1)写出图中全等的三角形,并加以证明.
(2)AD 与 BC 有怎样的位置关系?为什么?

答案:(1) $\triangle ABD \cong \triangle ACD$
证明:
因为$AD$平分$\angle BAC$,所以$\angle BAD = \angle CAD$。
在$\triangle ABD$和$\triangle ACD$中:
$AB = AC$(已知)
$\angle BAD = \angle CAD$(已证)
$AD = AD$(公共边)
根据$SAS$(边角边)判定定理,可得$\triangle ABD \cong \triangle ACD$。
(2) $AD\perp BC$
理由:
由(1)知$\triangle ABD \cong \triangle ACD$,所以$\angle ADB = \angle ADC$。
又因为$\angle ADB+\angle ADC = 180^{\circ}$,所以$\angle ADB=\angle ADC = 90^{\circ}$,即$AD\perp BC$。
两把大小不同的含 45°角的三角板 ABC,ADE 按如图所示方式放置,其中∠BAC= ∠DAE= 90°,点 B,C,E 在一条直线上,连接 DC.
(1)请找出图中的全等三角形,并说明理由;
(2)求证:DC⊥BE.

答案:(1)△ABE≌△ACD.
理由:∵△ABC和△ADE是含45°角的直角三角板,∠BAC=∠DAE=90°,
∴△ABC和△ADE是等腰直角三角形,
∴AB=AC,AD=AE.
∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD.
在△ABE和△ACD中,
$\left\{\begin{array}{l}AB=AC\\ \angle BAE=\angle CAD\\ AE=AD\end{array}\right.$,
∴△ABE≌△ACD(SAS).
(2)证明:∵△ABE≌△ACD,
∴∠ACD=∠ABE.
∵△ABC是等腰直角三角形,∠BAC=90°,
∴∠ABE=∠ACB=45°,
∴∠ACD=45°.
∵点B,C,E在一条直线上,
∴∠ACB+∠ACE=180°,
∴∠ACE=180°-∠ACB=180°-45°=135°.
∵∠ACE=∠ACD+∠DCE,
∴∠DCE=∠ACE-∠ACD=135°-45°=90°,
∴DC⊥BE.