1. 把x= -2代入代数式$2x^{2}-x-1$后的算式为
$2×(-2)^{2}-(-2)-1$
.
答案:$2×(-2)^{2}-(-2)-1$
解析:
将x=-2代入代数式$2x^{2}-x-1$,得$2×(-2)^{2}-(-2)-1$
2. 若$2a^{2}+3b+6= 8$,求代数式$2a^{2}+3b-9$的值.
答案:解$:$由题$,2a^{2}+3b=8-6=2$
则原式$=2-9=-7$
解析:
由$2a^{2}+3b+6=8$,得$2a^{2}+3b=8 - 6=2$。
将$2a^{2}+3b=2$代入$2a^{2}+3b - 9$,得$2 - 9=-7$。
$-7$
3. 已知$|a^{2}+b^{2}-3|= 5$,则$-3a^{2}-3b^{2}=$
-24
.
答案:-24
解析:
因为$|a^{2}+b^{2}-3|=5$,所以$a^{2}+b^{2}-3 = 5$或$a^{2}+b^{2}-3=-5$。
当$a^{2}+b^{2}-3 = 5$时,$a^{2}+b^{2}=8$;当$a^{2}+b^{2}-3=-5$时,$a^{2}+b^{2}=-2$。
因为$a^{2}\geq0$,$b^{2}\geq0$,所以$a^{2}+b^{2}\geq0$,故$a^{2}+b^{2}=-2$舍去,即$a^{2}+b^{2}=8$。
则$-3a^{2}-3b^{2}=-3(a^{2}+b^{2})=-3×8=-24$。
-24
4. 在一种计算游戏中,规定$\begin{vmatrix} a&b\\ c&d\end{vmatrix} = ad-bc$,则$\begin{vmatrix} 1&2\\ 3&4\end{vmatrix} $的值是
-2
.
答案:-2
5. 若a,b互为相反数,c,d互为倒数,$|m|= 4$,求代数式$(a+b)-dc+2cd-m^{2}+\frac{b}{a}$的值.
答案:解:由题,a+b=0,cd=1,m=±4
∴原式=0-1+2-16+(-1)=-16
解析:
因为a,b互为相反数,所以$a + b=0$,$\frac{b}{a}=-1$;
因为c,d互为倒数,所以$cd = 1$;
因为$|m|=4$,所以$m^{2}=16$。
原式$=0 - 1+2×1 - 16+(-1)$
$=0 - 1 + 2 - 16 - 1$
$=-16$
1. 小张在计算31+a的值时,误将“+”号看成“-”号,结果得12,那么31+a的值应为
50
.
答案:50
解析:
31 - a = 12
a = 31 - 12
a = 19
31 + a = 31 + 19 = 50
50
2. 某通信套餐的电话费与通话时间的关系如右表:
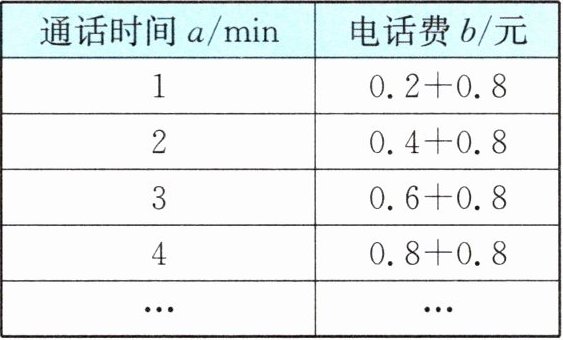
(1)试用含a的代数式表示b;
(2)当a= 100时,计算b的值.
答案:解:
(1)b=0.2a+0.8
(2)b=0.2×100+0.8=20.8
解析:
(1)$b = 0.2a + 0.8$
(2)当$a=100$时,$b=0.2×100 + 0.8=20.8$
3. 当x= 1时,代数式$px^{2}+qx+1$的值为2023. 请求出当x= -1时,代数式$px^{2}+qx+1$的值.
答案:解:由题,p+q+1=2023,∴p+q=2022
把x=-1代入原式=-p-q+1=-(p+q)+1=-2022+1=-2021
4. 根据表中弹簧长度与悬挂物体的质量的对应值,解答下列问题(假设均在弹簧弹性限度内):

(1)用代数式表示所挂物体的质量为x kg时的弹簧长度l(cm).
(2)所挂物体的质量为10 kg时,弹簧长度是多少?
(3)若测得弹簧长度是18 cm,则所挂物体的质量为多少?
(4)观察表格,随着悬挂物体的质量x逐渐增大,弹簧长度l如何变化?
答案:解:
(1)l=(0.5x+12)cm
(2)把x=10代入有,l=0.5×10+12=17,
∴为17cm
(3)把l=18代入有,18=0.5x+12,解得x=12,
∴为12kg
(4)l随着x的增大而增大