1. 已知$|a-1|+(b+2)^{2}= 0$,则$(a+b)^{2023}+a^{2024}$的值为
0
.
答案:0
解析:
因为$|a - 1| \geq 0$,$(b + 2)^2 \geq 0$,且$|a - 1| + (b + 2)^2 = 0$,所以$|a - 1| = 0$,$(b + 2)^2 = 0$。
由$|a - 1| = 0$,得$a - 1 = 0$,即$a = 1$。
由$(b + 2)^2 = 0$,得$b + 2 = 0$,即$b = - 2$。
则$a + b = 1 + (-2) = -1$。
所以$(a + b)^{2023} + a^{2024} = (-1)^{2023} + 1^{2024} = -1 + 1 = 0$。
0
2. 观察下列等式:
第1个等式$ a_{1}= \frac{1}{1× 4}= \frac{1}{3}× \left(1-\frac{1}{4}\right);$
第2个等式$ a_{2}= \frac{1}{4× 7}= \frac{1}{3}× \left(\frac{1}{4}-\frac{1}{7}\right);$
第3个等式$ a_{3}= \frac{1}{7× 10}= \frac{1}{3}× \left(\frac{1}{7}-\frac{1}{10}\right);$
第4个等式$ a_{4}= \frac{1}{10× 13}= \frac{1}{3}× \left(\frac{1}{10}-\frac{1}{13}\right);$
…请解答下列问题:(1)按以上规律列出第5个等式:a_{5}= __
$\frac{1}{13×16}$
__=__
$\frac{1}{3}× \left(\frac{1}{13}-\frac{1}{16}\right)$
__;(2)用含n的式子表示第n个等式:a_{n}= __
$\frac{1}{(3n-2)(3n+1)}$
__=__
$\frac{1}{3}\left(\frac{1}{3n-2}-\frac{1}{3n+1}\right)$
__(n为正整数);(3)求a_{1}+a_{2}+a_{3}+a_{4}+… +a_{100}的值.
$a_{1}+a_{2}+\cdots+a_{100}=\frac{1}{3}\left[\left(1-\frac{1}{4}\right)+\left(\frac{1}{4}-\frac{1}{7}\right)+\cdots+\left(\frac{1}{298}-\frac{1}{301}\right)\right]=\frac{1}{3}\left(1-\frac{1}{301}\right)=\frac{1}{3}×\frac{300}{301}=\frac{100}{301}$
答案:(1)$\frac{1}{13×16}$;$\frac{1}{3}×\left(\frac{1}{13}-\frac{1}{16}\right)$
(2)$\frac{1}{(3n-2)(3n+1)}$;$\frac{1}{3}\left(\frac{1}{3n-2}-\frac{1}{3n+1}\right)$
(3)$a_{1}+a_{2}+\cdots+a_{100}=\frac{1}{3}\left[\left(1-\frac{1}{4}\right)+\left(\frac{1}{4}-\frac{1}{7}\right)+\cdots+\left(\frac{1}{298}-\frac{1}{301}\right)\right]=\frac{1}{3}\left(1-\frac{1}{301}\right)=\frac{1}{3}×\frac{300}{301}=\frac{100}{301}$
3. 阅读材料:
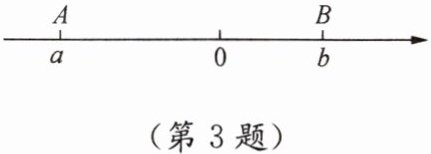
如图,若点$A$,$B在数轴上分别表示有理数a$,$b$,点$A$,$B之间的距离表示为AB$,则$AB= |a-b|$. 所以式子$|x-2|的几何意义是数轴上表示x$的点与表示 2 的点之间的距离.
根据上述材料,解答下列问题:
(1)式子$|x+1|$的几何意义是
数轴上表示$x$的点与表示$-1$的点之间的距离
,若$|x+1|= 2$,则$x= $
1 或 -3
.
(2)若$|x-3|= |x+1|$,则$x= $
1
.
(3)请说出$|x-3|+|x+1|= 7$表示的几何意义,并借助数轴求出$x$的值.
$\vert x - 3\vert + \vert x + 1\vert = 7$表示的几何意义是数轴上表示$x$的点到表示$3$的点与到表示$-1$的点的距离之和为$7$。
当$x \lt -1$时,$3 - x - x - 1 = 7$,
$2 - 2x = 7$,
$-2x = 5$,
解得$x = -2.5$;
当$-1\leqslant x\leqslant 3$时,$3 - x + x + 1 = 4\neq 7$,无解;
当$x \gt 3$时,$x - 3 + x + 1 = 7$,
$2x - 2 = 7$,
$2x = 9$,
解得$x = 4.5$。
综上,$x = -2.5$或$x = 4.5$。
(4)式子$|x-3|+|x+1|$是否有最小值?若有,请写出该最小值及此时$x$的取值范围.
有最小值。
当$x \lt -1$时,$\vert x - 3\vert + \vert x + 1\vert = 3 - x + (-x - 1) = 2 - 2x \gt 4$;
当$-1\leqslant x\leqslant 3$时,$\vert x - 3\vert + \vert x + 1\vert = 3 - x + x + 1 = 4$;
当$x \gt 3$时,$\vert x - 3\vert + \vert x + 1\vert = x - 3 + x + 1 = 2x - 2 \gt 4$。
所以最小值是$4$,此时$x$的取值范围是$-1\leqslant x\leqslant 3$。
答案:(1)
式子$\vert x + 1\vert$的几何意义是数轴上表示$x$的点与表示$-1$的点之间的距离。
因为$\vert x + 1\vert = 2$,所以$x + 1 = 2$或$x + 1 = -2$,
解得$x = 1$或$x = -3$。
(2)
因为$\vert x - 3\vert = \vert x + 1\vert$,所以$x - 3 = x + 1$(无解)或$x - 3 = -(x + 1)$,
由$x - 3 = -(x + 1)$,
$x - 3 = -x - 1$,
$2x = 2$,
解得$x = 1$。
(3)
$\vert x - 3\vert + \vert x + 1\vert = 7$表示的几何意义是数轴上表示$x$的点到表示$3$的点与到表示$-1$的点的距离之和为$7$。
当$x \lt -1$时,$3 - x - x - 1 = 7$,
$2 - 2x = 7$,
$-2x = 5$,
解得$x = -2.5$;
当$-1\leqslant x\leqslant 3$时,$3 - x + x + 1 = 4\neq 7$,无解;
当$x \gt 3$时,$x - 3 + x + 1 = 7$,
$2x - 2 = 7$,
$2x = 9$,
解得$x = 4.5$。
综上,$x = -2.5$或$x = 4.5$。
(4)
有最小值。
当$x \lt -1$时,$\vert x - 3\vert + \vert x + 1\vert = 3 - x + (-x - 1) = 2 - 2x \gt 4$;
当$-1\leqslant x\leqslant 3$时,$\vert x - 3\vert + \vert x + 1\vert = 3 - x + x + 1 = 4$;
当$x \gt 3$时,$\vert x - 3\vert + \vert x + 1\vert = x - 3 + x + 1 = 2x - 2 \gt 4$。
所以最小值是$4$,此时$x$的取值范围是$-1\leqslant x\leqslant 3$。