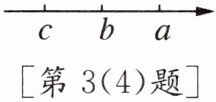3. 我们知道,对于有理数$a$,当$a>0$时,$|a|= a$;当$a<0$时,$|a|= -a$;当$a= 0$时,$|a|= a$.由此可知,对于$a-b$,若$a>b$,则$a-b>0$,即$|a-b|= a-b$;若$a<b$,则$a-b<0$,即$|a-b|= b-a$;若$a= b$,则$a-b= 0$,即$|a-b|= 0$.据此回答问题:
(1)在$|x-1|$中,当$x>1$时,$x-1$
>
0,$|x-1|= $
x-1
;
(2)在$|x-1|$中,当$x<1$时,$x-1$
<
0,$|x-1|= $
1-x
;
(3)在$|x-1|$中,当$x= 1$时,$x-1$
=
0,$|x-1|= $
0
;
(4)数$a$,$b$,$c$在数轴上表示的点如图所示,则$|b-a|= $
a-b
,$|b-c|= $
b-c
.