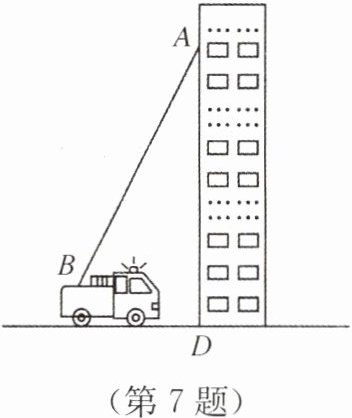
7. 防火安全无小事,时时处处需留心. 一天晚上,某居民楼的A处着火,消防大队派出云梯消防车展开紧急救援. 已知点A离地面28 m,消防车的云梯底部(点B)与地面的垂直距离是4 m,与居民楼的水平距离是10 m. 云梯需要伸长多少米才能到达着火处?
答案:作 $BC \perp$ 地面,垂足为 C,$BE \perp$ AD,垂足为 E,由题意得 $BC=4\ m$,$BE=10\ m$,$AD=28\ m$.$\therefore ED=BC=4\ m$,$AE=AD - ED=28 - 4=24(m)$.在$Rt\triangle ABE$中,由勾股定理,得$AB=\sqrt{AE^{2}+BE^{2}}=26(m)$.答:云梯需要伸长 26 m 才能到达着火处
解析:
作 $BC \perp$ 地面,垂足为 $C$,$BE \perp AD$,垂足为 $E$。由题意得 $BC=4\ m$,$BE=10\ m$,$AD=28\ m$。
$\therefore ED=BC=4\ m$,$AE=AD - ED=28 - 4=24\ (m)$。
在 $Rt\triangle ABE$ 中,由勾股定理,得 $AB=\sqrt{AE^{2}+BE^{2}}=\sqrt{24^{2}+10^{2}}=\sqrt{576 + 100}=\sqrt{676}=26\ (m)$。
答:云梯需要伸长 $26\ m$ 才能到达着火处。
8. 如图,透明圆柱形容器(容器厚度忽略不计)的高为15 cm,底面周长为8 cm,在容器内壁离容器底部6 cm的A处有一粒面包屑,此时一只蚂蚁正好在与A处相对的玻璃杯外壁,且距离容器顶部1 cm的B处,则蚂蚁要吃到面包屑需爬行的最短路径是多少厘米?

答案:如图,$AE=9\ cm$,$BD=9 + 1=10(cm)$,将容器侧面展开,作点 A 关于 EF 的对称点 $A'$,连接 $A'B$,则 $A'B$ 即为最短距离

$A'B=\sqrt{A'D^{2}+BD^{2}}=\sqrt{116}(cm)$
9. 某地气象台发布了台风蓝色预警,据报道,该次台风风力影响半径为250 km(即以台风中心为圆心,250 km为半径的圆形区域都会受台风影响). 如图,线段BC是台风中心从C市向西北方向移动到B市的大致路线,A处是某大型农场,且$AB\perp AC$. 若点A,C之间相距300 km,点A,B之间相距400 km.

(1) 判断A处的农场是否会受到台风的影响,并说明理由.
(2) 若台风中心的移动速度为25 km/h,则台风影响该农场持续时间有多长?
答案:
(1) 会受到台风的影响.理由:过点 A 作 $AD \perp BC$,垂足为 D.因为在 $Rt\triangle ABC$ 中,$AB \perp AC$,$AB=400\ km$,$AC=300\ km$,所以 $BC=\sqrt{AB^{2}+AC^{2}}=\sqrt{300^{2}+400^{2}}=500(km)$.因为 $AD \perp BC$,所以 $\frac{1}{2}BC \cdot AD=\frac{1}{2}AB \cdot AC$,所以 $AD=\frac{AB \cdot AC}{BC}=\frac{400 × 300}{500}=240(km)$.因为 $AD<250$,所以农场 A 会受到台风的影响
(2) 假设台风在线段 EF 上移动时,会对农场 A 造成影响,则 $AE=AF=250\ km$,$AD=240\ km$,由勾股定理,可得 $EF=2DF=2 × \sqrt{250^{2}-240^{2}}=2 × 70=140(km)$.因为台风的速度是 25 km/h,所以受台风影响的时间为 $140 ÷ 25=5.6(h)$