7. 图①是由三个正方形和一个直角三角形构成的图形,可以用其面积关系验证勾股定理。图②是把图①放入一个长方形内得到的,∠BAC= 90°,AB= 3,AC= 4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为
110
.
答案:110
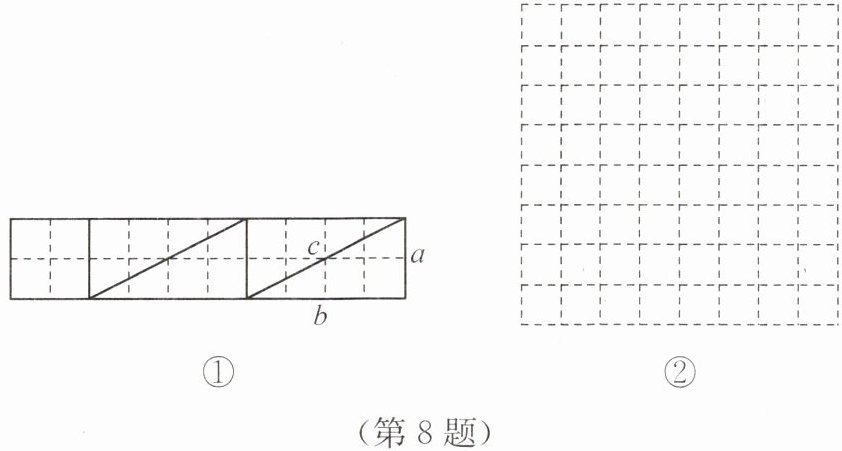
8. (1)图①是由20个边长为1的正方形组成的,把它按图①的分割方法分割成五部分后可拼接成一个大正方形(内部的粗实线表示分割线),请你在图②中画出拼接成的大正方形;
(2)如果(1)中分割成的直角三角形的两条直角边分别为a,b,斜边为c。请你利用图②证明勾股定理。
答案:(1)如图所示即为拼接成的大正方形
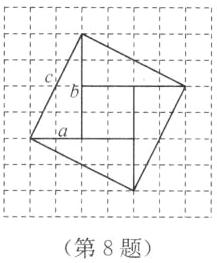
(2)$S_{大正方形}=4×\frac{1}{2}ab+(b-a)^2=2ab+b^2-2ab+a^2=a^2+b^2$,而$S_{大正方形}=c^2$,$\therefore a^2+b^2=c^2$
9. 意大利著名画家达·芬奇用如图所示的方法证明了勾股定理,其中图①的空白部分由两个正方形和两个直角三角形组成,图③的空白部分由两个直角三角形和一个正方形组成。设图①中空白部分的面积为$S_1$,图③中空白部分的面积为$S_2$.
(1)请用含a,b,c的代数式分别表示$S_1$,$S_2$;
(2)达·芬奇是如何利用该方法证明勾股定理的?

答案:(1)根据题意得,图①中空白部分的面积$S_1=a^2+b^2+2×\frac{1}{2}ab=a^2+b^2+ab$,图③中空白部分的面积$S_2=c^2+2×\frac{1}{2}ab=c^2+ab$ (2)由$S_1=S_2$,得$a^2+b^2+ab=c^2+ab$,$\therefore a^2+b^2=c^2$