8. 有一个直角三角形的两边长分别为4和5,则第三边的长为(
D
)
A.3
B.√41
C.3或√31
D.3或√41
答案:D
解析:
当4和5为直角边时,第三边长为$\sqrt{4^{2}+5^{2}}=\sqrt{41}$;
当5为斜边,4为直角边时,第三边长为$\sqrt{5^{2}-4^{2}}=3$。
D
9. 如图,观察作图过程,点A表示的实数为(
B
)
A.-√5
B.1-√5
C.-1+√5
D.-1-√5
答案:B
解析:
由图可知,以点1为圆心,点1到点3且垂直于数轴的点的距离为半径画弧,交数轴负半轴于点A。
点1到点3的水平距离为$3 - 1 = 2$,垂直距离为1,
则半径长为$\sqrt{2^2 + 1^2} = \sqrt{5}$,
点A到点1的距离为$\sqrt{5}$,且点A在点1左侧,
所以点A表示的实数为$1 - \sqrt{5}$。
B
10. 如图是“毕达哥拉斯树”的“生长”过程:如图①,一个边长为a的正方形,经过第一次“生长”后在它的上侧长出两个小正方形,面积分别为6和8,且三个正方形所围成的三角形是直角三角形,则a的值为
$\sqrt{14}$
;再经过一次“生长”后变成了图②.如此继续“生长”下去,第2024次“生长”后,这棵“毕达哥拉斯树”上所有正方形的面积之和为
28 350
.
答案:$\sqrt{14}$,28 350
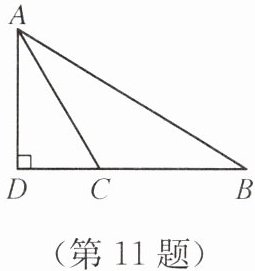
11. 如图,在△ABC中,AD是边BC上的高,AD= 12,BD= 16,CD= 5.求△ABC的周长.
答案:$\triangle ABC$ 的周长是 44
解析:
在$Rt\triangle ABD$中,$AD=12$,$BD=16$,由勾股定理得$AB=\sqrt{AD^{2}+BD^{2}}=\sqrt{12^{2}+16^{2}}=20$;
在$Rt\triangle ACD$中,$AD=12$,$CD=5$,由勾股定理得$AC=\sqrt{AD^{2}+CD^{2}}=\sqrt{12^{2}+5^{2}}=13$;
$BC=BD+CD=16+5=21$;
$\triangle ABC$的周长为$AB+BC+AC=20+21+13=54$。
12. 如图,方格纸中每个小正方形的边长都是1,分别按下列要求以格点为顶点画三角形.
(1)作出钝角三角形,使它的面积为4(在图①中画出一个即可),并计算你所画出的三角形三边的长.
(2)作面积为10的正方形(在图②中画出一个即可).

答案:(1)如图①所示,$\triangle ABC$ 即为面积为 4 的三角形;$AB=2$,$BC=\sqrt{32}$,$AC=\sqrt{20}$ (2)如图②所示
