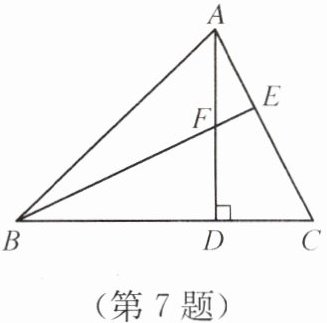
7. 如图,AD为△ABC的高,E为AC上一点,BE交AD于点F,且BF= AC,FD= CD. 求证:Rt△BFD≌Rt△ACD.
答案:
∵ AD 是△ABC 的高,
∴ ∠ADB=∠ADC=90°.在 Rt△BFD 和 Rt△ACD 中,{BF=AC,FD=CD},
∴ Rt△BFD≌Rt△ACD(HL)
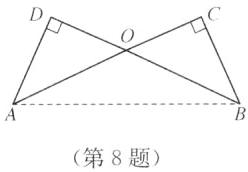
8. 如图,AC⊥BC,BD⊥AD,AD= BC. 求证:BD= AC.
小丽说:“可以利用‘AAS’证明.”小贾说:“可以利用‘HL’证明.”小雨说:“可以利用三角形的面积相等证明.”你认为他们的方法可行吗?如果可行,请选择一种方法进行证明.

答案:都可行. 证明①:
∵ AC⊥BC,BD⊥AD,
∴ ∠D=∠C=90°.在△AOD 和△BOC 中,{∠D=∠C,∠AOD=∠BOC,AD=BC},
∴ △AOD≌△BOC(AAS),
∴ AO=BO,DO=CO,
∴ AO+CO=BO+DO,即 BD=AC. 证明②:如图,连接 AB.
∵ AC⊥BC,BD⊥AD,
∴ ∠D=∠C=90°.在 Rt△ABD 和 Rt△BAC 中,{AD=BC,AB=BA},
∴ Rt△ABD≌Rt△BAC(HL).
∴ BD=AC.
证明③:连接 AB,由证明①知△AOD≌△BOC,
∴ S△AOD=S△BOC,
∴ S△AOD+S△AOB=S△BOC+S△AOB,即 S△ABD=S△ABC.
∵ S△ABD=$\frac{1}{2}$AD·BD,S△ABC=$\frac{1}{2}$BC·AC,
∴ $\frac{1}{2}$AD·BD=$\frac{1}{2}$BC·AC.
∵ AD=BC,
∴ BD=AC
9. CD是经过∠BCA顶点C的一条直线,CA= CB. 点E,F在直线CD上,且∠BEC= ∠CFA= ∠α.

(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请回答下列问题:
① 如图①,若∠BCA= 90°,∠α= 90°,则BE
=
CF;EF
=
|BE-AF|(填“>”“<”或“=”).
② 如图②,若0°<∠BCA<180°,添加一个关于∠α与∠BCA关系的条件:
∠α+∠BCA=180°
,可使①中的两个结论仍然成立. 请加以证明.
(2)如图③,若直线CD经过∠BCA的外部,∠α= ∠BCA,请对EF,BE,AF三条线段的数量关系作出合理猜想(不要求证明).
EF=BE+AF
答案:
(1) ① =,=. ② 所填的条件是∠α+∠BCA=180°.证明:在△BCE 中,∠CBE+∠BCE=180°-∠BEC=180°-∠α.
∵ ∠BCA=180°-∠α,
∴ ∠CBE+∠BCE=∠BCA.又
∵ ∠ACF+∠BCE=∠BCA,
∴ ∠CBE=∠ACF.
∵ BC=CA,∠BEC=∠CFA,
∴ △BCE≌△CAF(AAS).
∴ BE=CF,CE=AF.
∵ EF=CF-CE,
∴ EF=|BE-AF|
(2) 猜想 EF=BE+AF.
∵ ∠BEC=∠CFA=∠α,∠α=∠BCA,∠BCA+∠BCE+∠ACF=180°,∠CFA+∠CAF+∠ACF=180°,
∴ ∠BCE=∠CAF.又
∵ BC=CA,
∴ △BCE≌△CAF(AAS).
∴ BE=CF,EC=FA,
∴ EF=EC+CF=BE+AF