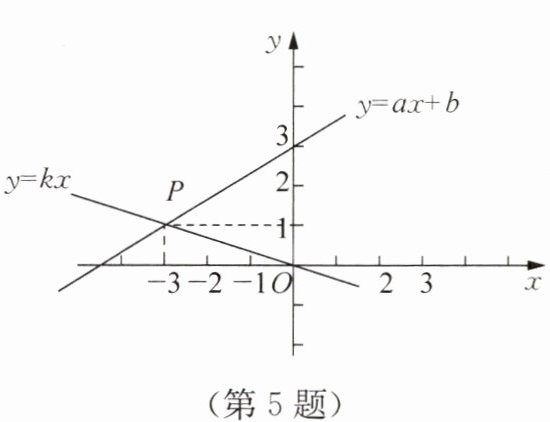
5. 如图,函数$y= ax+b和y= kx的图象交于点P$,根据图象可得关于$x$,$y的二元一次方程组\begin{cases}ax - y + b = 0 \\ kx - y = 0\end{cases} $的解是(
C
).
A.$\begin{cases}x= 3 \\ y= -1\end{cases} $
B.$\begin{cases}x= -3 \\ y= -1\end{cases} $
C.$\begin{cases}x= -3 \\ y= 1\end{cases} $
D.$\begin{cases}x= 3 \\ y= 1\end{cases} $
解析:
由图象可知,函数$y = ax + b$和$y = kx$的交点$P$的坐标为$(-3, 1)$。
因为二元一次方程组$\begin{cases}ax - y + b = 0 \\ kx - y = 0\end{cases}$可变形为$\begin{cases}y = ax + b \\ y = kx\end{cases}$,所以方程组的解就是两函数图象交点的坐标。
故该方程组的解是$\begin{cases}x = -3 \\ y = 1\end{cases}$。
C