13. 阅读材料并回答问题:
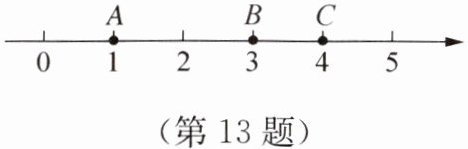
对于数轴上的三个点,若其中一个点与其他两个点的距离之间恰好满足2倍的数量关系,则称该点是其他两个点的“关联点”. 例如:如图,数轴上点A,B,C表示的数分别为1,3,4,点B与点A的距离是2,点B与点C的距离是1,此时点B是点A,C的“关联点”.
(1)若点P表示-2,点Q表示4. $-\frac{2}{3}$,0,2,6对应的点分别是$C_1$,$C_2$,$C_3$,$C_4$,则其中哪几个点是点P,Q的“关联点”?
$C_{2}$,$C_{3}$
(2)点M表示的数是-5,点N表示的数是15,P为数轴上一个动点. 若点P在点N的左侧,且点P是点M,N的“关联点”,则点P表示的数是______.
$-25$或$\frac{5}{3}$或$\frac{25}{3}$
答案:$(1) $解:$(1)C_{1}P=-\frac 23-(-2)=\frac 43,$$C_{1}Q=4-(-\frac 23)=\frac {14}{3} ,$$2C_{1}P≠C_{1}Q,$$C_{1}P≠2C_{1}Q,$
所以$C_{1}$不是点$P,$$Q $的$“$关联点$”;$
$C_{2}P=0-(-2)=2,$$C_{2}Q=4-0=4,$$2C_{2}P=C_{2}Q,$
所以$C_{2}$是点$P,$$Q $的$“$关联点$”;$
$C_{3}P=2-(-2)=4,$$C_{3}Q=4-2=2,$$C_{3}P=2C_{3}Q,$
所以$C_{3}$是点$P,$$Q $的$“$关联点$”;$
$C_{4}P=6-(-2)=8,$$C_{4}Q=6-4=2,$$2C_{4}P≠C_{4}Q,$$C_{4}P≠2C_{4}Q,$
所以$C_{4}$不是点$P,$$Q $的$“$关联点$”;$
综上所述,$C_{2},$$C_{3}$是点$P,$$Q $的$“$关联点$”.$
$(2) -25 $或$ \frac{5}{3}$或$\frac{25}{3}$